题目内容
已知圆(x-7)2+(y+4)2=16与圆(x+5)2+(y-6)2=16关于直线l对称,则直线l的方程是 .
【答案】分析:由已知圆(x-7)2+(y+4)2=16与圆(x+5)2+(y-6)2=16关于直线l对称,可得两圆的圆心关于l对称,从而可得圆心的连线被直线l垂直平分,由垂直平分线的定义,先求出线段的中点,再求出斜率,用点斜式整理可得直线方程.
解答:解:∵圆(x-7)2+(y+4)2=16与圆(x+5)2+(y-6)2=16关于直线l对称,
∴两圆的圆心P(7,-4),Q(-5,6)关于l对称,即PQ被直线L垂直平分
设PQ的中点为M(x,y)
由中点坐标公式:x=1,y=1
∵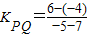 =
=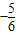
∴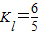
∴直线l的方程为y-1=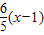
即6x-5y-1=0
故答案为:6x-5y-1=0
点评:本题主要考查垂直平分线的定义,一垂直即两直线的斜率互为负倒数,二平分即中点在垂直平分线上.
解答:解:∵圆(x-7)2+(y+4)2=16与圆(x+5)2+(y-6)2=16关于直线l对称,
∴两圆的圆心P(7,-4),Q(-5,6)关于l对称,即PQ被直线L垂直平分
设PQ的中点为M(x,y)
由中点坐标公式:x=1,y=1
∵
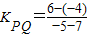 =
=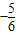
∴
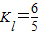
∴直线l的方程为y-1=
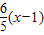
即6x-5y-1=0
故答案为:6x-5y-1=0
点评:本题主要考查垂直平分线的定义,一垂直即两直线的斜率互为负倒数,二平分即中点在垂直平分线上.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目