题目内容
在长为10,宽为6的矩形内画一个内切椭圆,切点为各边的中点,则此椭圆的离心率为( )
分析:由题设知此椭圆的长轴为10,短轴为6,由此能求出它的离心率.
解答:解:设椭圆方程为
+
=1,a>b>0
由题设知,2a=10,2b=6,
∴c=
=4,
∴e=
=
.
故选A.
| x2 |
| a2 |
| y2 |
| b2 |
由题设知,2a=10,2b=6,
∴c=
(
|
∴e=
| c |
| a |
| 4 |
| 5 |
故选A.
点评:本题考查椭圆的离心率的求法,解题要熟练掌握椭圆的简单性质,是基础题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成。已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米。
(1)若设休闲区的长![]() 米,求公园ABCD所占面积S关于
米,求公园ABCD所占面积S关于![]() 的函数
的函数![]() 的解析式;(6分 )
的解析式;(6分 )
 |
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?(6分 )

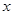 则长为
则长为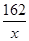 ,依题意,总造价
,依题意,总造价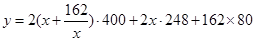
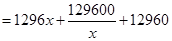
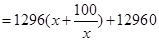
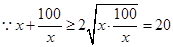 当且仅当
当且仅当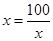 即
即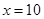 取等号
取等号
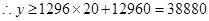 (元)得到结论。
(元)得到结论。