Question

用反证法证明：三角形的外角大于和它不相邻的任一内角.

Answer 1

解：已知：如下图所示，在△ABC中，∠ACD是外角.

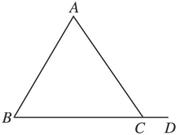
求证：∠ACD＞∠ABC.

 证明：假设∠ACD不大于∠BAC，则∠ACD=∠BAC或∠ACD＜∠BAC.

①若∠ACD=∠BAC，则由∠BAC与∠ACO互为内错角，知：AB∥CD,即AB与CD不相交，这与已知A、B、C是一个三角形的三个顶点相矛盾.

②若∠ACD＜∠BAC，

则在BC之间存在点B′使得∠B′AC=∠ACD.从△AB′C来看，又出现前面类似的矛盾.

所以假设不成立.故∠ACD＞∠ABC.