Question

（08年广东卷理）（本小题满分12分）设为实数，是方程的两个实根，数列满足，，（…）．

（1）证明：，；

（2）求数列的通项公式；

（3）若，，求的前项和．

Answer 1

【解析】（1）由求根公式，不妨设，得

，

（2）设，则，由得，

消去，得，是方程的根，由题意可知，

①当时，此时方程组的解记为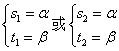

即、分别是公比为、的等比数列，

由等比数列性质可得,,

两式相减，得

，，

，

，即，

②当时，即方程有重根，，

即，得，不妨设，由①可知

，，

即，等式两边同时除以，得，即

数列是以1为公差的等差数列，

,

综上所述，

（3）把，代入，得，解得