题目内容
根据市气象站对春季某一天气温变化的数据统计显示,气温变化的分布与曲线y=Asin(
x+?)+b拟合(0≤x<24,单位为小时,y表示气温,单位为摄氏度,|?|<π,A>0),现已知这天气温为4至12摄氏度,并得知在凌晨1时整气温最低,下午13时整气温最高.
(1)求这条曲线的函数表达式;
(2)求下午19时整的气温.
| π |
| 12 |
(1)求这条曲线的函数表达式;
(2)求下午19时整的气温.
(1)由题意可知b=(4+12)÷2=8,A=12-8=4,
凌晨1时整气温最低,即x=1时函数取得最小值,∴
×1+?=-
+2kπ,k∈Z,|?|<π,
∴?=-
,13时整气温最高,
×13-
=
,函数取得最大值,满足题意,
所以这条曲线的函数表达式为:y=4sin(
x-
)+8.
(2)由(1)可知:x=19,y=4sin(
-
)+8=8,
所以下午19时整的气温为8摄氏度.
凌晨1时整气温最低,即x=1时函数取得最小值,∴
| π |
| 12 |
| π |
| 2 |
∴?=-
| 7π |
| 12 |
| π |
| 12 |
| 7π |
| 12 |
| π |
| 2 |
所以这条曲线的函数表达式为:y=4sin(
| π |
| 12 |
| 7π |
| 12 |
(2)由(1)可知:x=19,y=4sin(
| 19π |
| 12 |
| 7π |
| 12 |
所以下午19时整的气温为8摄氏度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 对春季某一天气温变化的数据统计显示,气温变化的分布可以用曲线
对春季某一天气温变化的数据统计显示,气温变化的分布可以用曲线 拟合(
拟合(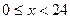 ,单位为小时,
,单位为小时,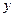 表示气温,单位为摄氏度,
表示气温,单位为摄氏度, ,
,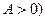 ,现已知这天气温为4至12摄氏度,并得知在凌晨1时整
,现已知这天气温为4至12摄氏度,并得知在凌晨1时整 气温最低,下午13时整气温最高。
气温最低,下午13时整气温最高。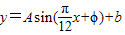 拟合(0≤x<24,单位为小时,y表示气温,单位为摄氏度,|ϕ|<π,A>0),现已知这天气温为4至12摄氏度,并得知在凌晨1时整气温最低,下午13时整气温最高.
拟合(0≤x<24,单位为小时,y表示气温,单位为摄氏度,|ϕ|<π,A>0),现已知这天气温为4至12摄氏度,并得知在凌晨1时整气温最低,下午13时整气温最高.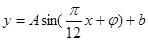 拟合(
拟合( ,单位为小时,
,单位为小时,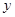 表示气温,单位为摄氏度,
表示气温,单位为摄氏度,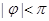 ,
,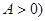 ,现已知这天气温为4至12摄氏度,并得知在凌晨1时整气温最低,下午13时整气温最高。
,现已知这天气温为4至12摄氏度,并得知在凌晨1时整气温最低,下午13时整气温最高。