题目内容
设P为锐角△ABC内任意一点,P点到三边BC、CA、AB的距离分别为PD、PE、PF,试求BD2+CE2+AF2的最小值.
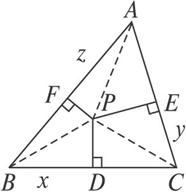
解:设BC=a,CA=b,AB=c,BD=x,CE=y,AF=z,如图,连结PA、PB、PC.
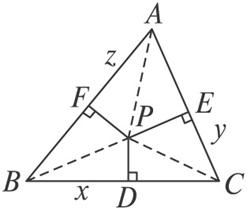
由勾股定理,得(x2+PD2)+(y2+PE2)+(z2+PF2)=PB2+PC2+PA2
=(c-z)2+PF2+(a-x)2+PD2+(b-y)2+PE2.
∴x2+y2+z2=(a-x)2+(b-y)2+(c-z)2,
即ax+by+cz=![]() (a2+b2+c2), ①
(a2+b2+c2), ①
由柯西不等式,得ax+by+cz≤![]() . ②
. ②
由①②,得![]() ≥
≥![]() (a2+b2+c2).
(a2+b2+c2).
∴x2+y2+z2≥![]() (a2+b2+c2),当且仅当x=λa,y=λb,z=λc时等号成立.
(a2+b2+c2),当且仅当x=λa,y=λb,z=λc时等号成立.
将它们代入①式,得λ=![]() .
.
∴当x=![]() ,y=
,y=![]() ,z=
,z=![]() ,即P为△ABC的外心时,BD2+CE2+AF2达到最小值
,即P为△ABC的外心时,BD2+CE2+AF2达到最小值![]() (a2+b2+c2).
(a2+b2+c2).

练习册系列答案
相关题目
 A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲
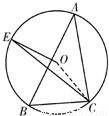
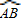 于点E,连接EC,求∠OEC.
于点E,连接EC,求∠OEC.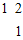 ]的作用下变换为曲线C2,求C2的方程.
]的作用下变换为曲线C2,求C2的方程.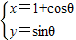 (θ为参数)上一点,求它到直线C2:
(θ为参数)上一点,求它到直线C2: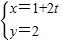 (t为参数)距离的最小值.
(t为参数)距离的最小值.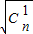 +
+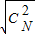 +L+
+L+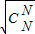 ≤
≤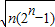 .
.