Question

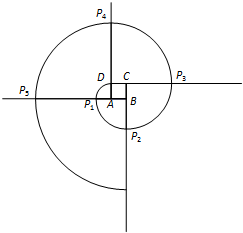（2011•丰台区二模）如图所示，已知正方形ABCD的边长为1，以A为圆心，AD长为半径画弧，交BA的延长线于P₁，然后以B为圆心，BP₁长为半径画弧，交CB的延长线于P₂，再以C为圆心，CP₂长为半径画弧，交DC的延长线于P₃，再以D为圆心，DP₃长为半径画弧，交AD的延长线于P₄，再以A为圆心，AP₄长为半径画弧，…，如此继续下去，画出的第8道弧的半径是

8

，画出第n道弧时，这n道弧的弧长之和为

n(n+1)π

4

．

Answer 1

分析：对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．通过分析找到各部分的变化规律后用一个统一的式子表示出变化规律是此类题目中的难点．

解答：解由题意知，第一道弧的长度为1，第二道弧的长度为2，第三道弧的长度为3，第四道弧的长度为4，第五道弧的长度5为5，第六道弧的长度为6，第七道弧的长度为7，第八道弧的长度为8，
第一段弧的长度为：

π

2

；
第二段的长度为：π；，
第三段的长度为：

3π

2

；
第四段的长度为：2π；
…
所以各段弧的长度构成一个以

π

2

为首项，以π为公差的等差数列，
所以这n道弧的弧长之和为

n(n+1)π

4

．
故答案为

n(n+1)π

4

点评：本题的关键是读懂题，读懂了就非常简单，主要考查了学生通过特例分析从而归纳总结出一般结论的能力．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．通过分析找到各部分的变化规律后直接利用规律求解．