题目内容
如果函数f(x)=sin(πx+θ)(0<θ<2π)的最小正周期是T,且当x=2时取得最大值,那么( )
A、T=2,θ=
| ||
| B、T=1,θ=π | ||
| C、T=2,θ=π | ||
D、T=1,θ=
|
分析:先根据三角函数周期公式求得T,再利用把x=2代入f(x)=sin(πx+θ)整理得f(x)=sinθ,进而可知当θ=
取最大值.
| π |
| 2 |
解答:解:T=
=2,
又当x=2时,sin(π•2+θ)=sin(2π+θ)=sinθ,
要使上式取得最大值,可取θ=
.
故选A
| 2π |
| π |
又当x=2时,sin(π•2+θ)=sin(2π+θ)=sinθ,
要使上式取得最大值,可取θ=
| π |
| 2 |
故选A
点评:本题主要考查了三角函数的周期性问题.属基础题.

练习册系列答案
相关题目
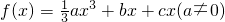 ,已知a<b<c,且
,已知a<b<c,且 ,曲线y=f(x)在x=1处取极值.
,曲线y=f(x)在x=1处取极值.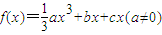 ,已知a<b<c,且
,已知a<b<c,且 ,曲线y=f(x)在x=1处取极值.
,曲线y=f(x)在x=1处取极值.