题目内容
(2013•和平区二模)设Sn为正项数列{an}的前n项和,且Sn=
an2+
an-
.
(I)求数列{an}的通项公式;
(II)设bn=
+
,且数列{bn}的前n项和Tn,证明:2n<Tn<2n+
.
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
(I)求数列{an}的通项公式;
(II)设bn=
| an+1 |
| an |
| an |
| an+1 |
| 2 |
| 3 |
分析:(I)再写一式,两式相减,结合{an}是正项数列,可得数列是等差数列,从而可求数列{an}的通项公式;
(II)确定数列的通项,利用基本不等式,结合裂项求和,即可证得结论.
(II)确定数列的通项,利用基本不等式,结合裂项求和,即可证得结论.
解答:(I)解:∵Sn=
an2+
an-
∴Sn-1=
an-12+
an-
(n≥2)
两式相减可得an=
(an2-an-12)+
(an-an-1)
∴(an+an-1)(an-an-1-2)=0
∵{an}是正项数列,∴an-an-1=2(n≥2)
∵a1=S1=
a12+
a1-
∴a1=3
∴an=3+2(n-1)=2n+1;
(II)证明:∵
>0,
>0,且
≠
∴bn=
+
=
+
>2
=2
∴Tn>2n
∵bn=
+
=2+2(
-
)
∴Tn=2n+2(
-
)+2(
-
)+…+2(
-
)=2n+2(
-
)<2n+
∴2n<Tn<2n+
.
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
∴Sn-1=
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
两式相减可得an=
| 1 |
| 4 |
| 1 |
| 2 |
∴(an+an-1)(an-an-1-2)=0
∵{an}是正项数列,∴an-an-1=2(n≥2)
∵a1=S1=
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
∴a1=3
∴an=3+2(n-1)=2n+1;
(II)证明:∵
| 2n+3 |
| 2n+1 |
| 2n+1 |
| 2n+3 |
| 2n+3 |
| 2n+1 |
| 2n+1 |
| 2n+3 |
∴bn=
| an+1 |
| an |
| an |
| an+1 |
| 2n+3 |
| 2n+1 |
| 2n+1 |
| 2n+3 |
|
∴Tn>2n
∵bn=
| 2n+3 |
| 2n+1 |
| 2n+1 |
| 2n+3 |
| 1 |
| 2n+1 |
| 1 |
| 2n+3 |
∴Tn=2n+2(
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2n+1 |
| 1 |
| 2n+3 |
| 1 |
| 3 |
| 1 |
| 2n+3 |
| 2 |
| 3 |
∴2n<Tn<2n+
| 2 |
| 3 |
点评:本题考查数列的通项与求和,考查裂项法的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
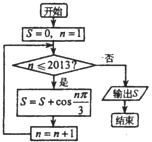 (2013•和平区二模)阅读如图所示的程序框图,运行相应的程序,则输出的结果S的值为( )
(2013•和平区二模)阅读如图所示的程序框图,运行相应的程序,则输出的结果S的值为( ) (2013•和平区二模)已知函数y=Asin(ωx+φ)(A>0,ω>0),|φ|<π)的部分图象如图所示,则它的解析式为( )
(2013•和平区二模)已知函数y=Asin(ωx+φ)(A>0,ω>0),|φ|<π)的部分图象如图所示,则它的解析式为( )