题目内容
设三棱柱的底面为正三角形,侧棱垂直于底面,一个体积是
的球与该棱柱的三个侧面和两个底面都相切,那么这个三棱柱的表面积是( )
| 32π |
| 3 |
分析:先确定球的半径,再求出正三棱柱的底面边长,即可求出三棱柱的表面积.
解答:解:∵球的体积是
,
∴球的半径为2,
∴正三棱柱的高h=2R=4.
设正三棱柱的底面边长为a,则其内切圆的半径为:
•
a=2,
∴a=4
.
∴三棱柱的表面积是2•
•(4
)2+3•4
•4=72
故选C.
| 32π |
| 3 |
∴球的半径为2,
∴正三棱柱的高h=2R=4.
设正三棱柱的底面边长为a,则其内切圆的半径为:
| 1 |
| 3 |
| ||
| 2 |
∴a=4
| 3 |
∴三棱柱的表面积是2•
| ||
| 4 |
| 3 |
| 3 |
| 3 |
故选C.
点评:本题考查了球的体积,柱体表面积公式的应用,的解题关键是求底面边长,属于中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
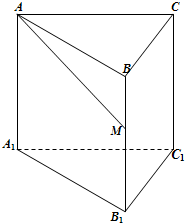 如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ.
如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ. 如图,正三棱柱ABC-A1B1C1中,底面边长为
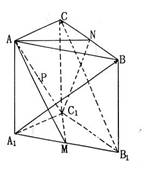
如图,正三棱柱ABC-A1B1C1中,底面边长为 如图,在正三棱柱ABC-A1B1C1中,点D,D1分别为棱BC,B1C1的中点.
如图,在正三棱柱ABC-A1B1C1中,点D,D1分别为棱BC,B1C1的中点. .
.

 ,NP
,NP 
 …………………………8分
…………………………8分 …………………………………9分
…………………………………9分
 ………………………………10分
………………………………10分
 的值,使
的值,使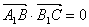 ;
;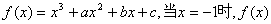 的极大值
的极大值