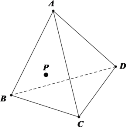
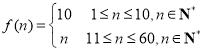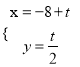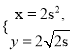题目内容
【题目】一个三位数：个位、十位、百位上的数字依次为
，
，
，当且仅当
，
时，称这样的数为“凸数”（如243），现从集合
中取出三个不同的数组成一个三位数，则这个三位数是“凸数”的概率为（ ）
A.
B.
C.
D.
【答案】B
【解析】
根据题意，分析“凸数”的定义，可得要得到一个满足
的三位“凸数”，在
的4个整数中任取3个不同数字，组成三位数，再将最大的放在十位上，剩余的2个数字分别放在百位、个位上即可，再利用古典概型概率计算公式即可得到所求的概率.
根据题意，要想得到一个满足的三位“凸数”，
在的4个整数中任取3个不同数字，
组成三位数，可有
种不同情况，
在在的4个整数中任取3个不同数字，
将最大的放在十位上，剩余的2个数字分别放在百位、个位上，
有
个不同的情况，
则这个三位数是“凸数”的概率是
，
故选：B.
练习册系列答案
相关题目
