题目内容
已知函数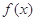 =
=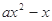 (
(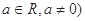 ,
,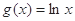
(1)当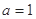 时,判断函数
时,判断函数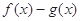 在定义域上的单调性;
在定义域上的单调性;
(2)若函数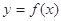 与
与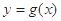 的图像有两个不同的交点
的图像有两个不同的交点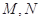 ,求
,求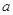 的取值范围。
的取值范围。
(3)设点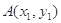 和
和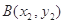 (
(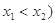 是函数
是函数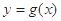 图像上的两点,平行于
图像上的两点,平行于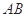 的切线以
的切线以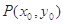 为切点,求证
为切点,求证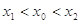 .
.
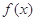 =
=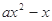 (
(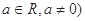 ,
,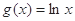
(1)当
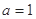 时,判断函数
时,判断函数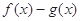 在定义域上的单调性;
在定义域上的单调性;(2)若函数
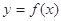 与
与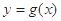 的图像有两个不同的交点
的图像有两个不同的交点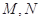 ,求
,求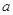 的取值范围。
的取值范围。(3)设点
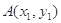 和
和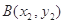 (
(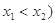 是函数
是函数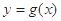 图像上的两点,平行于
图像上的两点,平行于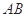 的切线以
的切线以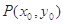 为切点,求证
为切点,求证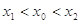 .
.(1)在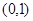 上单调递减,在
上单调递减,在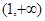 上单调递增;(2)
上单调递增;(2)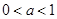 ;(3)证明见解析.
;(3)证明见解析.
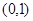 上单调递减,在
上单调递减,在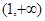 上单调递增;(2)
上单调递增;(2)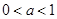 ;(3)证明见解析.
;(3)证明见解析.试题分析:
解题思路:(1)求导,利用导数的正负确定函数的单调区间;(2)构造函数,将图像的交点个数转化为函数的零点个数,通过函数的极值的正负求参数的值;(3)构造函数,利用放缩法合理转化.
规律总结:利用导数研究函数的单调性、极值、最值及与函数有关的综合题,都体现了导数的重要性;此类问题往往从求导入手,思路清晰;但综合性较强,需学生有较高的逻辑思维和运算能力.
试题解析:(1)记
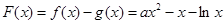 ,则
,则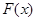 的定义域为
的定义域为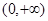 .
.当
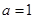 时,
时,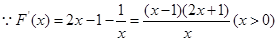 ,
,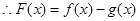 在
在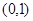 上单调递减,在
上单调递减,在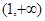 上单调递增.
上单调递增.由
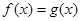 得
得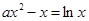 ,即
,即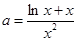 ,
,令
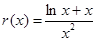 ,
,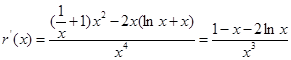 ;
;当
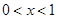 时,
时,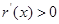 ,则
,则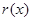 单调递增,且
单调递增,且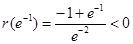 ;
;当
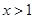 时,
时,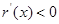 ,则
,则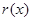 单调递减,且
单调递减,且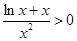 ,
,所以
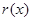 在
在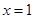 处取到最大值
处取到最大值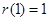 ;
;故要使
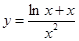 与
与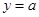 有两个不同的交点,只需
有两个不同的交点,只需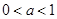 .
.(3)由已知:
 ,所以
,所以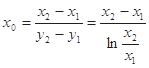
由
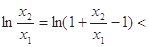
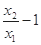 ,故
,故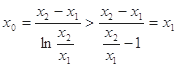
同理
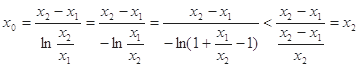
综上所述得
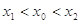 .
. 
练习册系列答案
相关题目
 在
在 上是增函数.
上是增函数. 的取值范围
的取值范围 ;
;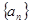 满足:
满足: ,且
,且 ,
, ,并判断
,并判断 与
与 的大小.
的大小. 满足:
满足: ,且对任意
,且对任意 满足
满足 ,
, 的解集为( ).
的解集为( ).



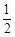 x
x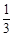 x
x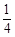 x
x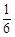 x
x 的图象经过点
的图象经过点 ,
, 、
、 (
( )是函数图象上的任意不同两点,给出以下结论:
)是函数图象上的任意不同两点,给出以下结论: ;②
;② ;③
;③ ;④
;④ .
.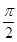 )上不是凸函数的是________.
)上不是凸函数的是________.