题目内容
若方程mx2-3x-3=0在 上有解,则m的取值范围是 .
上有解,则m的取值范围是 .
【答案】分析:由题意可得m≠0,令f(x)=mx2-3x-3,若方程mx2-3x-3=0在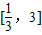 上有1个解,可得f(
上有1个解,可得f( )f(3)≤0,由此求得≤m的范围.若方程mx2-3x-3=0在
)f(3)≤0,由此求得≤m的范围.若方程mx2-3x-3=0在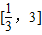 上有2个解,可得
上有2个解,可得 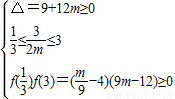 .由此求得m的范围.再把求得的这两个m的范围取并集,即得所求.
.由此求得m的范围.再把求得的这两个m的范围取并集,即得所求.
解答:解:当m=0时,解得x=-1,不满足条件,故m≠0.
由题意可得方程mx2-3x-3=0在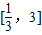 上有1个解或有2个解.
上有1个解或有2个解.
令f(x)=mx2-3x-3,若方程mx2-3x-3=0在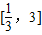 上有1个解,可得f(
上有1个解,可得f( )f(3)≤0,
)f(3)≤0,
即 (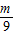 -4)(9m-12)≤0,解得
-4)(9m-12)≤0,解得 ≤m≤36.
≤m≤36.
若方程mx2-3x-3=0在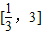 上有2个解,可得
上有2个解,可得 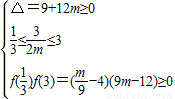 .
.
解得 ≤m≤
≤m≤ .
.
综上可得,得 ≤m≤36,
≤m≤36,
故答案为[ ,36].
,36].
点评:本题主要考查一元二次方程根的分布与系数的关系,二次函数的性质应用,属于中档题.
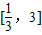 上有1个解,可得f(
上有1个解,可得f( )f(3)≤0,由此求得≤m的范围.若方程mx2-3x-3=0在
)f(3)≤0,由此求得≤m的范围.若方程mx2-3x-3=0在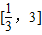 上有2个解,可得
上有2个解,可得 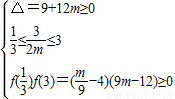 .由此求得m的范围.再把求得的这两个m的范围取并集,即得所求.
.由此求得m的范围.再把求得的这两个m的范围取并集,即得所求.解答:解:当m=0时,解得x=-1,不满足条件,故m≠0.
由题意可得方程mx2-3x-3=0在
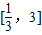 上有1个解或有2个解.
上有1个解或有2个解.令f(x)=mx2-3x-3,若方程mx2-3x-3=0在
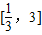 上有1个解,可得f(
上有1个解,可得f( )f(3)≤0,
)f(3)≤0,即 (
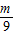 -4)(9m-12)≤0,解得
-4)(9m-12)≤0,解得 ≤m≤36.
≤m≤36.若方程mx2-3x-3=0在
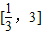 上有2个解,可得
上有2个解,可得 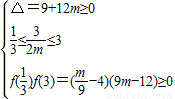 .
.解得
 ≤m≤
≤m≤ .
.综上可得,得
 ≤m≤36,
≤m≤36,故答案为[
 ,36].
,36].点评:本题主要考查一元二次方程根的分布与系数的关系,二次函数的性质应用,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目