题目内容
已知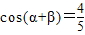
，
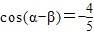，则cosα•cosβ=（ ）A．1
B．-1
C．
D．0
【答案】分析：把已知条件利用两角和差的余弦公式展开，再把得到的这两个式子相加可得 2cosαcosβ=0，从而得到 cosαcosβ=0．
解答：解：由已知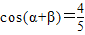
，
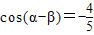可得 cosαcosβ-sinαsinβ=
，cosαcosβ+sinαsinβ=-
．
把得到的这两个式子相加可得 2cosαcosβ=0，
∴cosαcosβ=0，
故选D．
点评：本题主要考查两角和差的余弦公式的应用，属于基础题．
解答：解：由已知
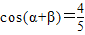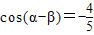，可得 cosαcosβ-sinαsinβ=，cosαcosβ+sinαsinβ=-．把得到的这两个式子相加可得 2cosαcosβ=0，
∴cosαcosβ=0，
故选D．
点评：本题主要考查两角和差的余弦公式的应用，属于基础题．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
已知α∈R，则cos(
+α)=（ ）
| π |
| 2 |
| A、sinα | B、cosα |
| C、-sinα | D、-cosα |
,θ∈(-
,0),则cos(θ-
)的值为( )
B.
C.-
D.
,π),sin(α+β)=-
,sin(β-
)=
,则cos(α+
)=____________.