题目内容
 已知椭圆
已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)若椭圆的焦距为2
| 3 |
8
| ||
| 3 |
(Ⅱ)在(I)的条件下,椭圆上有一点M,满足MF1⊥MF2,求△MF1F2的面积;
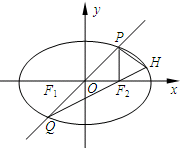
(Ⅲ)过焦点F2作椭圆长轴的垂线与椭圆交于第一象限点P,连接PO并延长交椭圆于点Q,连接QF2并延长交椭圆于点H,若PH⊥PQ,求椭圆的离心率.
分析:(Ⅰ)由椭圆的焦距可求c,再由两条准线间的距离为
可求a,利用条件b2=a2-c2求出b2,则椭圆的方程可求;
(Ⅱ)因为点M在椭圆上,利用椭圆定义得到MF1+MF2=4,由MF1⊥MF2得到MF12+MF22=12两式联立得到MF1•MF2=2,则△MF1F2的面积可求;
(Ⅲ)首先求出P点坐标,利用对称性求出Q点坐标,写出直线QF2的方程后和椭圆联立求出H的坐标,然后利用PH和PQ所在直线的斜率之积等于-1得到a,b的关系式,则离心率可求.
8
| ||
| 3 |
(Ⅱ)因为点M在椭圆上,利用椭圆定义得到MF1+MF2=4,由MF1⊥MF2得到MF12+MF22=12两式联立得到MF1•MF2=2,则△MF1F2的面积可求;
(Ⅲ)首先求出P点坐标,利用对称性求出Q点坐标,写出直线QF2的方程后和椭圆联立求出H的坐标,然后利用PH和PQ所在直线的斜率之积等于-1得到a,b的关系式,则离心率可求.
解答:解:(Ⅰ)由题意可知2c=2
,∴c=
,
由
=
,得a2=
c=
×
=4,
∴b2=a2-c2=4-3=1.
即椭圆的方程为
+y2=1;
(Ⅱ)由椭圆定义得MF1+MF2=4 ①
因为MF1⊥MF2,所以MF12+MF22=12 ②
将①2-②:得MF1•MF2=2
故△MF1F2的面积S=
|MF1|•|MF2|=
×2=1;
(Ⅲ)把x=c代入椭圆
+
=1,得y=
=
,
所以点P的坐标为(c,
),则Q(-c,-
),F2(c,0),
直线QF2方程为
=
,即y=
(x-c),
与椭圆
+
=1联立得H点坐标为(
,
),
由PH⊥PQ得,kPQ•kPH=-1,即
•
=-1,
化简得a2=2b2,
即 a2=2(a2-c2),即 e2=
,又0<e<1,所以e=
.
| 3 |
| 3 |
由
| 2a2 |
| c |
8
| ||
| 3 |
4
| ||
| 3 |
4
| ||
| 3 |
| 3 |
∴b2=a2-c2=4-3=1.
即椭圆的方程为
| x2 |
| 4 |
(Ⅱ)由椭圆定义得MF1+MF2=4 ①
因为MF1⊥MF2,所以MF12+MF22=12 ②
将①2-②:得MF1•MF2=2
故△MF1F2的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅲ)把x=c代入椭圆
| x2 |
| a2 |
| y2 |
| b2 |
b2(1-
|
| b2 |
| a |
所以点P的坐标为(c,
| b2 |
| a |
| b2 |
| a |
直线QF2方程为
| y-0 | ||
-
|
| x-c |
| -c-c |
| b2 |
| 2ac |
与椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| 4a2c-b2c |
| 4c2+b2 |
| b4 |
| a(4c2+b2) |
由PH⊥PQ得,kPQ•kPH=-1,即
| b2 |
| ac |
| ||||
|
化简得a2=2b2,
即 a2=2(a2-c2),即 e2=
| 1 |
| 2 |
| ||
| 2 |
点评:本题考查了椭圆的标准方程,考查了直线和圆锥曲线的关系,该题思路清晰,运算复杂,考查了学生的运算能力.属难题.

练习册系列答案
相关题目