题目内容
已知函数f(x)=ex+2 ﹣3x.
﹣3x.
(1)求曲线y=f(x)在点(1,f (1))处的切线方程;
(2)当x≥1时,若关于x的不等式f(x)≥
 +(a﹣3)x+1恒成立,试求实数a的取值范围.
+(a﹣3)x+1恒成立,试求实数a的取值范围.
 ﹣3x.
﹣3x.(1)求曲线y=f(x)在点(1,f (1))处的切线方程;
(2)当x≥1时,若关于x的不等式f(x)≥

 +(a﹣3)x+1恒成立,试求实数a的取值范围.
+(a﹣3)x+1恒成立,试求实数a的取值范围.解:(1)f'(x)=ex+4x﹣3
则f'(1)=e+1,
又f(1)=e﹣1
∴曲线y=f(x)在点(1,f (1))处的切线方程为y﹣e+1=(e+1)(x﹣1)
即(e+1)x﹣y﹣2=0
(2)由f(x)≥
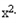 +(a﹣3)x+1得ex+2
+(a﹣3)x+1得ex+2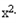 ﹣3x≥
﹣3x≥
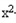 +(a﹣3)x+1
+(a﹣3)x+1
即ax≤ex﹣
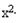 ﹣1
﹣1
∵x≥1
∴a≤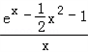
记g(x)=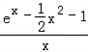 ,则g'(x)=
,则g'(x)=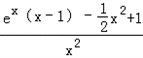
记φ(x)=ex(x﹣1)﹣
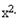 +1
+1
则φ'(x)=x(ex﹣1)
∵x≥1,φ'(x)>0,
∴φ(x)在[1,+∞)上单调递增
∴g(x)≥φ(1)= >0
>0
∴g'(x)>0,
∴g(x)在[1,+∞)上单调递增
∴g(x)≥g(1)=e﹣
由a≤g(x)恒成立,得a≤g(x)min,
∴a≤e﹣ 即a的取值范围是(﹣∞,e﹣
即a的取值范围是(﹣∞,e﹣ ]
]
则f'(1)=e+1,
又f(1)=e﹣1
∴曲线y=f(x)在点(1,f (1))处的切线方程为y﹣e+1=(e+1)(x﹣1)
即(e+1)x﹣y﹣2=0
(2)由f(x)≥

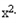 +(a﹣3)x+1得ex+2
+(a﹣3)x+1得ex+2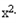 ﹣3x≥
﹣3x≥
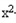 +(a﹣3)x+1
+(a﹣3)x+1即ax≤ex﹣

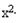 ﹣1
﹣1∵x≥1
∴a≤
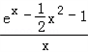
记g(x)=
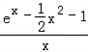 ,则g'(x)=
,则g'(x)=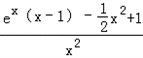
记φ(x)=ex(x﹣1)﹣

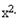 +1
+1则φ'(x)=x(ex﹣1)
∵x≥1,φ'(x)>0,
∴φ(x)在[1,+∞)上单调递增
∴g(x)≥φ(1)=
 >0
>0∴g'(x)>0,
∴g(x)在[1,+∞)上单调递增
∴g(x)≥g(1)=e﹣

由a≤g(x)恒成立,得a≤g(x)min,
∴a≤e﹣
 即a的取值范围是(﹣∞,e﹣
即a的取值范围是(﹣∞,e﹣ ]
]
练习册系列答案
相关题目