题目内容
已知函数f(x)=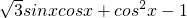 .
.
(Ⅰ)求f(x)的最小正周期、对称轴方程及单调区间;
(Ⅱ)现保持纵坐标不变,把f(x)图象上所有点的横坐标伸长到原来的4倍,得到新的函数h(x);
(ⅰ)求h(x)的解析式;
(ⅱ)△ABC中,角A、B、C的对边分别为a、b、c,且满足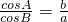 ,h(A)=
,h(A)= ,c=2,试求△ABC的面积.
,c=2,试求△ABC的面积.
解:(I)∵f(x)=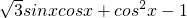 =
= sin2x-
sin2x- =sin2xcos
=sin2xcos +cos2xsin
+cos2xsin -
- ,
,
∴f(x)=sin(2x+ )-
)- ,f(x)的最小正周期为T=
,f(x)的最小正周期为T= =π.
=π.
令2x+ =
= +kπ,得x=
+kπ,得x= +
+ kπ,k∈Z,所以函数图象的对称轴方程为:x=
kπ,k∈Z,所以函数图象的对称轴方程为:x= +
+ kπ,(k∈Z)
kπ,(k∈Z)
令- +2kπ≤2x+
+2kπ≤2x+ ≤
≤ +2kπ,解之得-
+2kπ,解之得- +kπ≤x≤
+kπ≤x≤ +kπ,所以函数的单调增区间为[-
+kπ,所以函数的单调增区间为[- ,
, +kπ],(k∈Z)
+kπ],(k∈Z)
同理可得,函数的单调减区间为[ +kπ,
+kπ, +kπ],(k∈Z)
+kπ],(k∈Z)
(II)∵保持纵坐标不变,把f(x)图象上所有点的横坐标伸长到原来的4倍,得到新的函数h(x)
∴h(x)=f( x)=sin(
x)=sin( x+
x+ )-
)- ,
,
(i)h(x)的解析式为h(x)=sin( x+
x+ )-
)- ;
;
(ii)∵h(A)=sin( A+
A+ )-
)- =
= ,
,
∴sin( A+
A+ )=
)= ,结合A∈(0,π)得A=
,结合A∈(0,π)得A=
∵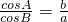 =
=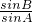
∴sinAcosA=sinBcosB,可得sin2A=sin2B,即A=B或A+B=
①当A=B时,因为c=2,A= ,所以△ABC是边长为2的等边三角形,
,所以△ABC是边长为2的等边三角形,
因此,△ABC的面积S= ×22=
×22= .
.
②当A+B= 时,因为c=2,A=
时,因为c=2,A= ,所以△ABC是斜边为2的直角三角形
,所以△ABC是斜边为2的直角三角形
∴a=csinA=2× =
= ,b=ccosA=2×
,b=ccosA=2× =1
=1
因此,△ABC的面积S= ×
× ×1=
×1= .
.
综上所述,得△ABC的面积是 或
或 .
.
分析:(I)利用二倍角的三角函数公式降次,再用辅助角公式合并得f(x)=sin(2x+ )-
)- ,再结合函数y=Asin(ωx+φ)的图象与性质的有关公式,可得f(x)的最小正周期、对称轴方程及单调区间;
,再结合函数y=Asin(ωx+φ)的图象与性质的有关公式,可得f(x)的最小正周期、对称轴方程及单调区间;
(II)(i)根据函数y=Asin(ωx+φ)的图象变换的公式,不难得到h(x)的解析式为h(x)=sin( x+
x+ )-
)- ;
;
(ii)根据h(A)的值结合三角形内角的范围和特殊三角函数的值,求得A= ,再由
,再由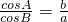 结合正弦定理,讨论得三角形是等腰三角形或是直角三角形,最后在两种情况下分别解此三角形,再结合面积公式可求出△ABC的面积.
结合正弦定理,讨论得三角形是等腰三角形或是直角三角形,最后在两种情况下分别解此三角形,再结合面积公式可求出△ABC的面积.
点评:本题综合了三角恒变换、函数y=Asin(ωx+φ)的图象变换、利用正余弦定理解三角形等知识,对三角函数的知识进行了综合考查,是一道中档题.
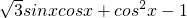 =
= sin2x-
sin2x- =sin2xcos
=sin2xcos +cos2xsin
+cos2xsin -
- ,
,∴f(x)=sin(2x+
 )-
)- ,f(x)的最小正周期为T=
,f(x)的最小正周期为T= =π.
=π.令2x+
 =
= +kπ,得x=
+kπ,得x= +
+ kπ,k∈Z,所以函数图象的对称轴方程为:x=
kπ,k∈Z,所以函数图象的对称轴方程为:x= +
+ kπ,(k∈Z)
kπ,(k∈Z)令-
 +2kπ≤2x+
+2kπ≤2x+ ≤
≤ +2kπ,解之得-
+2kπ,解之得- +kπ≤x≤
+kπ≤x≤ +kπ,所以函数的单调增区间为[-
+kπ,所以函数的单调增区间为[- ,
, +kπ],(k∈Z)
+kπ],(k∈Z)同理可得,函数的单调减区间为[
 +kπ,
+kπ, +kπ],(k∈Z)
+kπ],(k∈Z)(II)∵保持纵坐标不变,把f(x)图象上所有点的横坐标伸长到原来的4倍,得到新的函数h(x)
∴h(x)=f(
 x)=sin(
x)=sin( x+
x+ )-
)- ,
,(i)h(x)的解析式为h(x)=sin(
 x+
x+ )-
)- ;
;(ii)∵h(A)=sin(
 A+
A+ )-
)- =
= ,
,∴sin(
 A+
A+ )=
)= ,结合A∈(0,π)得A=
,结合A∈(0,π)得A=
∵
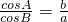 =
=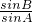
∴sinAcosA=sinBcosB,可得sin2A=sin2B,即A=B或A+B=

①当A=B时,因为c=2,A=
 ,所以△ABC是边长为2的等边三角形,
,所以△ABC是边长为2的等边三角形,因此,△ABC的面积S=
 ×22=
×22= .
.②当A+B=
 时,因为c=2,A=
时,因为c=2,A= ,所以△ABC是斜边为2的直角三角形
,所以△ABC是斜边为2的直角三角形∴a=csinA=2×
 =
= ,b=ccosA=2×
,b=ccosA=2× =1
=1因此,△ABC的面积S=
 ×
× ×1=
×1= .
.综上所述,得△ABC的面积是
 或
或 .
.分析:(I)利用二倍角的三角函数公式降次,再用辅助角公式合并得f(x)=sin(2x+
 )-
)- ,再结合函数y=Asin(ωx+φ)的图象与性质的有关公式,可得f(x)的最小正周期、对称轴方程及单调区间;
,再结合函数y=Asin(ωx+φ)的图象与性质的有关公式,可得f(x)的最小正周期、对称轴方程及单调区间;(II)(i)根据函数y=Asin(ωx+φ)的图象变换的公式,不难得到h(x)的解析式为h(x)=sin(
 x+
x+ )-
)- ;
;(ii)根据h(A)的值结合三角形内角的范围和特殊三角函数的值,求得A=
 ,再由
,再由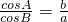 结合正弦定理,讨论得三角形是等腰三角形或是直角三角形,最后在两种情况下分别解此三角形,再结合面积公式可求出△ABC的面积.
结合正弦定理,讨论得三角形是等腰三角形或是直角三角形,最后在两种情况下分别解此三角形,再结合面积公式可求出△ABC的面积.点评:本题综合了三角恒变换、函数y=Asin(ωx+φ)的图象变换、利用正余弦定理解三角形等知识,对三角函数的知识进行了综合考查,是一道中档题.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|