题目内容
已知P，Q为抛物线x2＝2y上两点，点P，Q的横坐标分别为4，－2，过P，Q分别作抛物线的切线，两切线交于点A，则点A的纵坐标为________．
－4
解析 由已知可设P(4，y1)，Q(－2，y2)，
∵点P，Q在抛物线x2＝2y上，
∴
∴P(4,8)，Q(－2,2)．
又∵抛物线可化为y＝
x2，∴y′＝x.
∴过点P的切线斜率为y′|x＝4＝4.
∴过点P的切线为y－8＝4(x－4)，即y＝4x－8.
又∵过点Q的切线斜率为y′|x＝－2＝－2，
∴过点Q的切线为y－2＝－2(x＋2)，即y＝－2x－2.
联立
得x＝1，y＝－4.
∴点A的纵坐标为－4.
练习册系列答案
53随堂测系列答案
相关题目
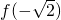是f（x）的极小值，
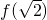是f（x）的极大值；
=（1，1），
=（1，-1），则向量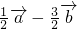
=（-2，-1）；
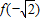是f（x）的极小值，
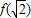是f（x）的极大值；
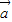=（1，1），
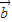=（1，-1），则向量
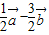=（-2，-1）；