题目内容
已知函数f(x)=x+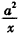 ,g(x)=x+lnx,其中a>0.
,g(x)=x+lnx,其中a>0.
(Ⅰ)若x=1是函数h(x)=f(x)+g(x)的极值点,求实数a的值;
(Ⅱ)若对任意的x1,x2∈[1,e](e为自然对数的底数)都有f(x1)≥g(x2)成立,求实数a的取值范围。
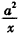 ,g(x)=x+lnx,其中a>0.
,g(x)=x+lnx,其中a>0. (Ⅰ)若x=1是函数h(x)=f(x)+g(x)的极值点,求实数a的值;
(Ⅱ)若对任意的x1,x2∈[1,e](e为自然对数的底数)都有f(x1)≥g(x2)成立,求实数a的取值范围。
解:(Ⅰ)因为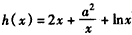 ,其定义域为
,其定义域为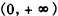 ,
,
所以,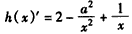 ,
,
由x=1是函数h(x)的极值点,得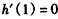 ,即3-a2=0,
,即3-a2=0,
又由a>0,得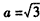 ,
,
经检验,当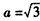 时,x=1是函数h(x)的极值点,
时,x=1是函数h(x)的极值点,
所以,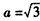 。
。
(Ⅱ)若对任意的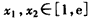 都有
都有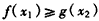 成立等价于
成立等价于
对任意的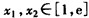 都有
都有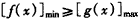 ,
,
当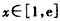 时,
时,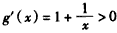 ,所以函数g(x)在
,所以函数g(x)在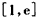 上是增函数,
上是增函数,
所以,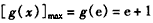 ,
,
又由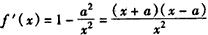 ,且
,且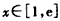 ,a>0,
,a>0,
(1)当0<a<1且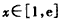 时,
时,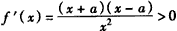 ,
,
所以函数f(x)在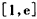 上是增函数,
上是增函数,
所以,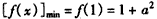 ,
,
由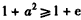 ,得
,得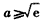 ,
,
又由0<a<1知a不合题意,舍去;
(2)当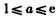 时,
时,
若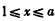 ,则
,则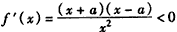 ;
;
若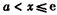 ,则
,则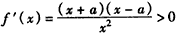 ,
,
所以函数f(x)在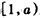 上是减函数,在
上是减函数,在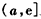 上是增函数,
上是增函数,
所以,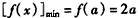 ,
,
由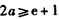 ,得
,得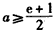 ,
,
又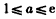 ,所以,
,所以,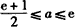 ;
;
(3)当a>e且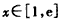 时,
时,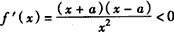 ,
,
所以函数f(x)在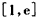 上是减函数,
上是减函数,
所以,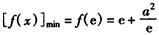 ,
,
由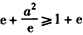 ,得
,得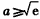 ,
,
又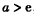 ,所以
,所以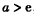 ;
;
综上所述,a的取值范围是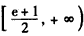 。
。
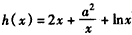 ,其定义域为
,其定义域为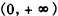 ,
,所以,
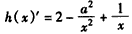 ,
,由x=1是函数h(x)的极值点,得
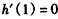 ,即3-a2=0,
,即3-a2=0,又由a>0,得
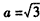 ,
,经检验,当
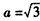 时,x=1是函数h(x)的极值点,
时,x=1是函数h(x)的极值点,所以,
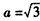 。
。(Ⅱ)若对任意的
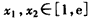 都有
都有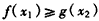 成立等价于
成立等价于对任意的
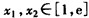 都有
都有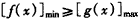 ,
,当
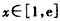 时,
时,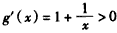 ,所以函数g(x)在
,所以函数g(x)在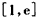 上是增函数,
上是增函数,所以,
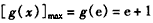 ,
,又由
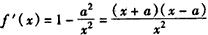 ,且
,且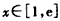 ,a>0,
,a>0,(1)当0<a<1且
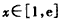 时,
时,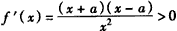 ,
,所以函数f(x)在
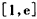 上是增函数,
上是增函数,所以,
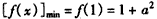 ,
,由
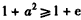 ,得
,得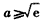 ,
,又由0<a<1知a不合题意,舍去;
(2)当
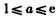 时,
时,若
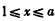 ,则
,则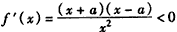 ;
;若
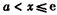 ,则
,则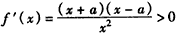 ,
,所以函数f(x)在
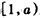 上是减函数,在
上是减函数,在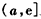 上是增函数,
上是增函数,所以,
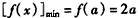 ,
,由
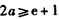 ,得
,得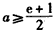 ,
,又
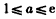 ,所以,
,所以,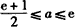 ;
;(3)当a>e且
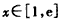 时,
时,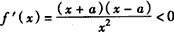 ,
,所以函数f(x)在
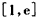 上是减函数,
上是减函数,所以,
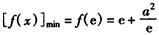 ,
,由
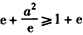 ,得
,得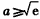 ,
,又
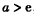 ,所以
,所以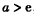 ;
;综上所述,a的取值范围是
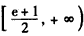 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目