周长为20的矩形绕其一边旋转形成一个圆柱.该圆柱的侧面积的最大值是( )A．25πB．50πC．100πD．200π 题目和参考答案——青夏教育精英家教网—

题目内容

9．周长为20的矩形绕其一边旋转形成一个圆柱，该圆柱的侧面积的最大值是（　　）

A．

25π

B．

50π

C．

100π

D．

200π

分析根据题意，设出矩形的长、宽，求出圆柱的侧面积，再利用基本不等式，即可求得结论．

解答解：设矩形的长、宽分别是x，y，则x+y=10，
所以圆柱的侧面积S_侧=2πxy=2π$\sqrt{xy}$²≤2π（$\frac{x+y}{2}$）²=2π×25=50π．
当且仅当x=y=5时，取“=”号．
∴当矩形的长、宽都是5时，旋转所形成的圆柱侧面积最大值是50π．
故选：B

点评本题考查圆柱的侧面积，考查基本不等式的运用，注意基本不等式的使用条件是解题的关键．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

20．某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数：
①sin²13°+cos²17°-sin13°cos17°；
②sin²15°+cos²15°-sin15°cos15°；
③sin²18°+cos²12°-sin18°cos12°；
④sin²（-30°）+cos²60°-sin（-30°）cos60°；
⑤sin²（-25°）+cos²55°-sin（-25°）cos55°．
（1）试从上述五个式子中选择一个，求出这个常数；
（2）根据（1）的计算结果，将该同学的发现推广到一个三角恒等式，并证明你的结论．

17．某商场在今年“十一”黄金周期间采取购物抽奖的方式促销（每人至多抽奖一次），设了金奖和银奖，奖券共2000张．在某一时段对30名顾客进行调查，其中有$\frac{2}{3}$的顾客没有得奖，而得奖的顾客中有$\frac{3}{5}$的顾客得银奖，若对这30名顾客随机采访3名顾客．
（1）求选取的3名顾客中至少有一人得金奖的概率；
（2）求选取的3名顾客中得金奖人数不多于得银奖人数的概率．

4．若{a_n}是等比数列，a_n＞0，且a₂a₄+2a₃a₅+a₄a₆=25，那么a₃+a₅的值为（　　）

14．

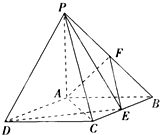如图所示，四棱锥P-ABCD中，底面ABCD是矩形，PA⊥底面ABCD，PA=AB=1，AD=$\sqrt{3}$，点F是PB的中点，点E在棱BC上移动．
（Ⅰ）当E为BC的中点时，试判断EF与平面PAC的位置关系，并说明理由；
（Ⅱ）当BE为何值时，PA与平面PDE所成角的大小为45°？

1．在复平面内，与复数z=-3+4i的共轭复数对应的点位于（　　）

18．已知函数y=f（x）的定义域为{x|-3≤x≤8，且x≠5}，值域为{y|-1≤y≤2，且y≠0}．下列关于函数y=f（x）的说法：①当x=-3时，y=-1；②点（5，0）不在函数y=f（x）的图象上；③将y=f（x）的图象补上点（5，0），得到的图象必定是一条连续的曲线；④y=f（x）是[-3，5）上的单调函数．⑤y=f（x）的图象与坐标轴只有一个交点．其中一定正确的说法的序号为②③．

19．已知直线ax+4y-2=0与2x-5y+b=0互相垂直，垂足为（1，c），则a+b+c的值为（　　）

试题分类