题目内容
已知y=f(x)是定义在区间(-∞,0)∪(0,+∞)上的奇函数,且在(0,+∞)上是增函数,f(1)=0.
(1)解不等式f(x)≥0;
(2)设函数g(x)=-x2+mx-2m(x∈[0,1],m∈R),集合M={m|g(x)<0},集合N={m|f[g(x)]<0},求M∩N.
解析:
|
解:(1)因为f(x)为定义在区间(-∞,0)∪(0,+∞)上的奇函数且f(1)=0,所以f(-x)=-f(x),则f(-1)=-f(1)=0; 当x∈(0,+∞)时,因为f(x)在(0,+∞)上是增函数,由f(x)≥0得x≥1; 因为奇函数在关于原点对称的区间上单调性相同,又f(x)在(0,+∞)上是增函数,所以f(x)在区间(-∞,0)上也是增函数,又因为f(-1)=0,所以当x∈(-∞,0)时,由f(x)≥0得-1≤x<0. 综上所述,不等式f(x)≥0的解集为[-1,0)∪[1,+∞). (2)由(1)可知f(x)≥0的解集为[-1,0)∪[1,+∞),因为f(x)的定义域为(-∞,0)∪(0,+∞),所以f(x)<0的解集为(-∞,-1)∪(0,1).所以由f[g(x)]<0得g(x)<-1或0<g(x)<1,即N={m|g(x)<-1或0<g(x)<1},因为M={m|g(x)<0},所以M∩N={m|g(x)<-1}.因为g(x)=-x2+mx-2m(x∈[0,1]),所以g(x)<-1化为-x2+mx-2m+1<0,即(x-2)m+1-x2<0,因为x∈[0,1],所以m> 点评:本题所给函数是抽象函数,具有一定的综合性;在解决第一问时可以借助函数的单调性与奇偶性画出草图来帮助我们解题;在解决第二问时,可能有学生会分别求出集合M与N,然后再取交集,教师应该引导学生按照以上解答过程来解决省时省力. |
提示:
|
本题中的函数f(x)是抽象函数,因此只能由函数的性质,结合函数的草图来解决本题. |

 +2at)x+3at+b=0,直线l的
+2at)x+3at+b=0,直线l的 ,则当t为何值时,f(t)有最大值,最大值是多少?
,则当t为何值时,f(t)有最大值,最大值是多少? )在曲线C上,又在直线l上,求
)在曲线C上,又在直线l上,求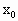 的取值范围.
的取值范围.

 是x=x0为极值点的既不充分也不必要条件;
是x=x0为极值点的既不充分也不必要条件; , 则
, 则 (其中
(其中 );
);