题目内容
11.若函数f(x)=x2+ax+b对任意正整数n,有f(n)<f(n+1),则a的取值范围是多少?分析 若对任意正整数n,有f(n)<f(n+1),则函数f(x)=x2+ax+b对称轴$-\frac{a}{2}$<$\frac{1+2}{2}$,进而得到答案.
解答 解:函数f(x)=x2+ax+b的图象是开口朝上,且以直线x=$-\frac{a}{2}$为对称轴的抛物线,
若对任意正整数n,有f(n)<f(n+1),
则$-\frac{a}{2}$<$\frac{1+2}{2}$,
解得:a>-3
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
19.下面说法错误的是( )
| A. | 数乘向量就是一个实数λ与向量$\overrightarrow{a}$的乘积 | |
| B. | λ>0,λ$\overrightarrow{a}$就是把$\overrightarrow{a}$同方向放大或缩小 | |
| C. | λ$\overrightarrow{a}$就是把$\overrightarrow{a}$沿反方向放大或缩小 | |
| D. | λ=0,则$λ\overrightarrow{a}$=$\overrightarrow{0}$ |
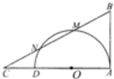 如图,已知AD为半圆O的直径,AB为半圆O的切线,割线BMN交AD的延长线于点C,且BM=MN=NC,AB=2$\sqrt{2}$.
如图,已知AD为半圆O的直径,AB为半圆O的切线,割线BMN交AD的延长线于点C,且BM=MN=NC,AB=2$\sqrt{2}$.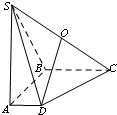 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB⊥BC,侧棱SA⊥底面ABCD,点O为侧棱SC的中点,且SA=AB=BC=2,AD=1.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB⊥BC,侧棱SA⊥底面ABCD,点O为侧棱SC的中点,且SA=AB=BC=2,AD=1.