题目内容
设m,n(m≠n)是函数f(x)=ax3+bx2-a2x(a>0)的两个极值点.
(1)若m=-1,n=2,求函数f(x)解析式;
(2)若|m|+|n|=2
,求b的最大值.
(1)若m=-1,n=2,求函数f(x)解析式;
(2)若|m|+|n|=2
| 2 |
分析:(1)由f(x)=ax3+bx2-a2x(a>0),知f'(x)=3ax2+2bx-a2(a>0)依题意有
,由此能求出f(x).
(2)先对函数进行求导,根据函数f(x)=ax3+bx2-a2x(a>0)的两个极值点为m,n(m≠n),可以得到△>0且由韦达定理可得m+n,mn,把等式转化为关于m+n,mn的关系式,求出a、b的关系,把a看成未知数x,求三次函数的最值,利用导数求极值,是b2最大值,开方可求b的最大值.
|
(2)先对函数进行求导,根据函数f(x)=ax3+bx2-a2x(a>0)的两个极值点为m,n(m≠n),可以得到△>0且由韦达定理可得m+n,mn,把等式转化为关于m+n,mn的关系式,求出a、b的关系,把a看成未知数x,求三次函数的最值,利用导数求极值,是b2最大值,开方可求b的最大值.
解答:解:(1)∵f(x)=ax3+bx2-a2x(a>0),
∴f'(x)=3ax2+2bx-a2(a>0)
依题意有
,
∴
(a>0).
解得
,
∴f(x)=6x3-9x2-36x.
(2)∵f'(x)=3ax2+2bx-a2(a>0),
依题意,m,n是方程f'(x)=0的两个根,
且|m|+|n|=2
,
∴(m+n)2-2mn+2|mn|=8.
∴(-
)2-2•(-
)+2|-
|=8,
∴b2=3a2(6-a)
∵b2≥0,
∴0<a≤6,
设p(a)=3a2(6-a),
则p′(a)=-9a2+36a.
由p'(a)>0得0<a<4,
由p'(a)<0得a>4.
即:函数p(a)在区间(0,4]上是增函数,
在区间[4,6]上是减函数,
∴当a=4时,p(a)有极大值为96,
∴p(a)在(0,6]上的最大值是96,
∴b的最大值为4
.
∴f'(x)=3ax2+2bx-a2(a>0)
依题意有
|
∴
|
解得
|
∴f(x)=6x3-9x2-36x.
(2)∵f'(x)=3ax2+2bx-a2(a>0),
依题意,m,n是方程f'(x)=0的两个根,
且|m|+|n|=2
| 2 |
∴(m+n)2-2mn+2|mn|=8.
∴(-
| 2b |
| 3a |
| a |
| 3 |
| a |
| 3 |
∴b2=3a2(6-a)
∵b2≥0,
∴0<a≤6,
设p(a)=3a2(6-a),
则p′(a)=-9a2+36a.
由p'(a)>0得0<a<4,
由p'(a)<0得a>4.
即:函数p(a)在区间(0,4]上是增函数,
在区间[4,6]上是减函数,
∴当a=4时,p(a)有极大值为96,
∴p(a)在(0,6]上的最大值是96,
∴b的最大值为4
| 6 |
点评:本题考查函数解析式的求法和实数b的最大值的求法.由原函数极值点的个数判断出导函数解的个数,利用判别式得参数的关系,用韦达定理把参数和解联系起来,韦达定理是个很好的“桥梁”,求最大值要先求极大值,三次函数一般用导数来求.

练习册系列答案
相关题目
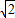 ,求b的最大值.
,求b的最大值.