Question

已知数列{a_n}满足a_n＞0,且对一切n∈N^*,有=S_n²,其中S_n=.

(1)求证:对一切n∈N^*,有a_n+1²-a_n+1=2S_n;

(2)求数列{a_n}的通项公式;

(3)求证:＜3.

Answer 1

解析:(1)由=S_n²,①?

则=S_n+1².②?

②-①,得a_n+1³=S_n+1²-S_n²=(S_n+1+S_n)(S_n+1-S_n)=(2S_n+a_n+1)a_n+1?.?

因为a_n+1＞0,所以a_n+1²-a_n+1=2S_n.?

(2)由a_n+1²-a_n+1=2S_n及a_n²-a_n=2S_n-1(n≥2),?

两式相减,得(a_n+1+a_n)(a_n+1-a_n)=a_n+1+a_n.?

因为a_n+1+a_n＞0,所以a_n+1-a_n=1(n≥2).?

当n=1,2时易得a₁=1,a₂=2,所以a_n+1-a_n=1(n≥1).?

所以{a_n}是以a₁=1为首项,d=1为公差的等差数列.?

故a_n=n.?

(3) = ＜1+?

＜1+?

=1+?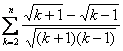

=1+?

=1+1+ - -?

＜2+＜3.