题目内容
如图，
，双曲线M是以B、C为焦点且过A点.(Ⅰ)建立适当的坐标系，求双曲线M的方程；(Ⅱ)设过点E(1,0)的直线l分别与双曲线M的左、右支交于F、G两点，直线l的斜率为k，求k的取值范围.；
（Ⅲ）对于（II）中的直线l，是否存在k
使|OF|=|OG|
若有求出k的值，若没有说明理由．（O为原点）
(Ⅰ) 
(Ⅱ) 
（Ⅲ）
解析:
：（I）以BC边的中点为原点，BC边所在直线为x轴，建立直角坐标系，…1分
则
，得
…3分设双曲线方程为
……5分
（II）当
轴时，l与双曲线无交点.当l不垂直x轴时，可设l的方程：
由
，消去y，得
……7分
与双曲线的左、右两支分别交于
则
…10分
（Ⅲ）若|OF|=|OG|，三角形OFG中，设M是FG的中点，则有：OM
……12分
由（II）易得
，中点M（
则应有：
使|OF|=|OG|．14分
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
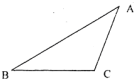如图，
，双曲线M是以B、C为焦点且过A点．
，双曲线M是以B、C为焦点且过A点.
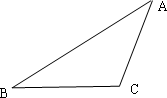
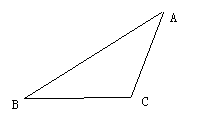(Ⅰ)建立适当的坐标系，求双曲线M的方程；
使|OF|=|OG|
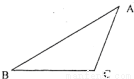如图，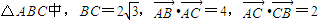
，双曲线M是以B、C为焦点且过A点．