题目内容
已知F1,F2是两个定点,椭圆C1和等轴双曲线C2都以F1,F2为焦点.点P是C1和C2的一个交点,且 ,那么椭圆C1的离心率为( )
,那么椭圆C1的离心率为( )A.
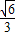
B.

C.

D.

【答案】分析:设等轴双曲线的半实轴长为 ,F1P=x,F2P=y,不妨设x>y,通过双曲线的定义,得到一个方程,利用
,F1P=x,F2P=y,不妨设x>y,通过双曲线的定义,得到一个方程,利用 得到圆的一个方程,求出x,y;通过椭圆的定义,求出椭圆的离心率.
得到圆的一个方程,求出x,y;通过椭圆的定义,求出椭圆的离心率.
解答:解:设等轴双曲线的半实轴长为 ,F1P=x,F2P=y,不妨设x>y,则x-y=
,F1P=x,F2P=y,不妨设x>y,则x-y= …①,
…①,
又 ,∴∠F1PF2=90°,所以x2+y2=(2c)2,…②,解①②得x=
,∴∠F1PF2=90°,所以x2+y2=(2c)2,…②,解①②得x= ,y=
,y= ,
,
再根椐椭圆定义,2a=x+y= ,(2a表示椭圆长轴长),得e=
,(2a表示椭圆长轴长),得e= =
= .
.
故选A.
点评:本题是中档题,考查椭圆与双曲线的关系,注意椭圆与双曲线的定义的应用是解题的关键,考查计算能力.
 ,F1P=x,F2P=y,不妨设x>y,通过双曲线的定义,得到一个方程,利用
,F1P=x,F2P=y,不妨设x>y,通过双曲线的定义,得到一个方程,利用 得到圆的一个方程,求出x,y;通过椭圆的定义,求出椭圆的离心率.
得到圆的一个方程,求出x,y;通过椭圆的定义,求出椭圆的离心率.解答:解:设等轴双曲线的半实轴长为
 ,F1P=x,F2P=y,不妨设x>y,则x-y=
,F1P=x,F2P=y,不妨设x>y,则x-y= …①,
…①,又
 ,∴∠F1PF2=90°,所以x2+y2=(2c)2,…②,解①②得x=
,∴∠F1PF2=90°,所以x2+y2=(2c)2,…②,解①②得x= ,y=
,y= ,
,再根椐椭圆定义,2a=x+y=
 ,(2a表示椭圆长轴长),得e=
,(2a表示椭圆长轴长),得e= =
= .
.故选A.
点评:本题是中档题,考查椭圆与双曲线的关系,注意椭圆与双曲线的定义的应用是解题的关键,考查计算能力.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
已知F1、F2是两个定点,点P是以F1和F2为公共焦点的椭圆和双曲线的一个交点,并且PF1⊥PF2,e1和e2分别是上述椭圆和双曲线的离心率,则有( )
| A、e12+e22=2 | ||||||||
| B、e12+e22=4 | ||||||||
C、
| ||||||||
D、
|