题目内容
已知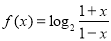
(1)判断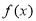 奇偶性并证明;
奇偶性并证明;
(2)判断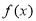 单调性并用单调性定义证明;
单调性并用单调性定义证明;
(3)若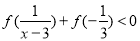 ,求实数
,求实数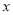 的取值范围.
的取值范围.
(1)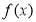 为
为 上的奇函数;(2)
上的奇函数;(2)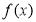 在
在 上单调递增;(3)
上单调递增;(3)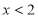 或
或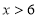 .
.
【解析】
试题分析:(1)证明函数的奇偶性步骤:第一步,判断定义域是否关于原点对称,本题中函数的定义域为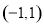 ,关于原点对称;第二步,判断
,关于原点对称;第二步,判断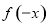 与
与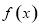 的关系,本题中
的关系,本题中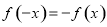 ,所以原函数为
,所以原函数为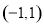 上的奇函数;(2)本题中利用定义证明函数的单调性步骤:第一步,任取
上的奇函数;(2)本题中利用定义证明函数的单调性步骤:第一步,任取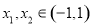 且
且 ,再比较
,再比较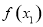 与
与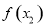 的大小关系,得到
的大小关系,得到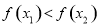 ,所以
,所以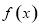 在
在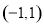 上单调递增得证;(3)解不等式一种是直接法,一种是单调性法.本题中用后者比较简单,首先移项,利用函数为奇函数,将原不等式变形为
上单调递增得证;(3)解不等式一种是直接法,一种是单调性法.本题中用后者比较简单,首先移项,利用函数为奇函数,将原不等式变形为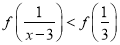 ,再利用单调性,同解变形为
,再利用单调性,同解变形为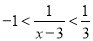 ,进一步解得结果.
,进一步解得结果.
试题解析:(1) 定义域为
定义域为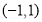 ,关于原点对称. 2分
,关于原点对称. 2分
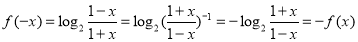

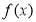 为
为 上的奇函数. 4分
上的奇函数. 4分
设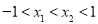
则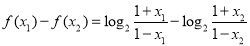
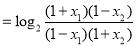
又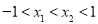
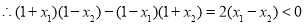
即
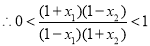
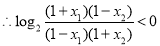
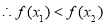
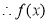 在
在 上单调递增. 8分
上单调递增. 8分
(3)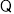
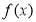 为
为 上的奇函数.
上的奇函数. 
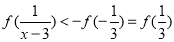
又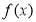 在
在 上单调递增.
上单调递增.
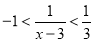
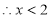 或
或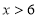 . 12分
. 12分
考点:1.函数奇偶性的判断;(2)函数单调性的定义;(3)利用函数奇偶性和单调性解不等式.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 的图形的一条对称轴经过点( ) .
的图形的一条对称轴经过点( ) .



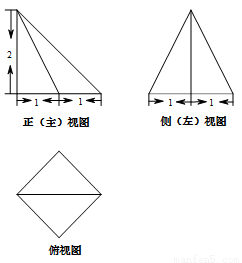
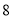 B.
B. C.
C.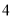 D.
D.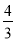
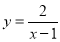 的定义域是(-∞,1)∪[2,5),则其值域是( )
的定义域是(-∞,1)∪[2,5),则其值域是( ) 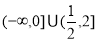 B.(-∞,2]
B.(-∞,2]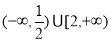 D.(0,+∞)
D.(0,+∞)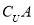 ={2},则集合A的真子集共有( )
={2},则集合A的真子集共有( ) .
.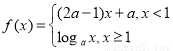 是
是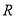 上的减函数,则实数
上的减函数,则实数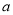 的取值范围是( )
的取值范围是( )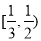 B.
B.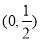 C.
C.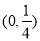 D.
D.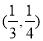
 的方程为
的方程为 ,圆
,圆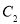 的方程
的方程 ,过
,过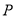 作圆
作圆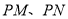 ,切点分别为
,切点分别为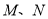 ,则
,则 的最大值为
的最大值为 B.
B. C.
C. D.
D.
 的解集为_______
的解集为_______