Question

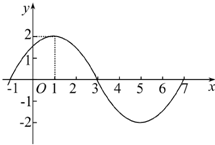已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜

π

2

，x∈R）的图象的一部分如图所示．
（1）求函数f（x）的解析式；
（2）当x∈[-4，-

2

3

]时，求函数y=f（2）+f（x+2）的最大值与最小值及相应的x的值．

Answer 1

分析：（1）由图象知A=2，T=8，进而可得ω=

π

4

，代入点（1，2）的坐标可得φ值，可得解析式；
（2）代入化简可得y=

2

+2cos（

π

4

x+

π

4

），由x∈[-4，-

2

3

]结合三角函数的运算，逐步求解可得．

解答：解：（1）由图象知A=2，T=8，
∵T=

2π

ω

=8，∴ω=

π

4

，
又图象经过点（1，2），∴2sin（

π

4

+φ）=1．
∴φ=2kπ+

π

4

，k∈Z，
∵|φ|＜

π

2

，∴φ=

π

4

，
∴f（x）=2sin（

π

4

x+

π

4

）
（2）y=f（2）+f（x+2）
=

2

+2sin（

π

4

x+

π

2

+

π

4

）
=

2

+2cos（

π

4

x+

π

4

），
∵x∈[-4，-

2

3

]，∴-

3π

4

≤

π

4

x+

π

2

≤

π

12

．
∴当

π

4

x+

π

4

=-

3π

4

，即x=-4时，y=f（2）+f（x+2）取得最小值0；
当

π

4

x+

π

4

=0，即x=-1时，y=f（2）+f（x+2）取得最大值2

2

点评：本题考查三角函数解析式的求解，涉及三角函数的最值得求解，属中档题．