题目内容

如图，边长为1的正方体ABCD-A1B1C1D1，P是棱CC1上任一点，CP=m(0＜m＜1)。

(Ⅰ)若m=，求证：面BPD1⊥面BDD1B1；

(Ⅱ)试确定m值，使直线AP与平面BDD1B1所成角的正切值为.

答案：证明：(Ⅰ)连B1D交BD1于M,∴M为四边形BDD1B1中心,连PM∵P为CC1中点

(Ⅱ)以CD为x轴,CB为y轴,CC1为z轴,建立直角坐标系,C(0,0,0),A(1,1,0),P(0,0,m)

=(-1,-1,m)而面BB1D1B法向量为=(1,1,0)设与面BB1D1B所成角为θ,

∴sinθ=|ocs|

而tanθ=,cotθ=∴1+cot20=  解得m=.

练习册系列答案
相关题目
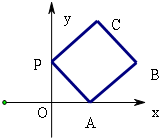精英家教网（北京卷理14）如图放置的边长为1的正方形PABC沿x轴滚动．设顶点p（x，y）的轨迹方程是y=f（x），则f（x）的最小正周期为
 
；y=f（x）在其两个相邻零点间的图象与x轴所围区域的面积为
 

说明：“正方形PABC沿X轴滚动”包括沿x轴正方向和沿x轴负方向滚动．沿x轴正方向滚动指的是先以顶点A为中心顺时针旋转，当顶点B落在x轴上时，再以顶点B为中心顺时针旋转，如此继续．类似地，正方形PABC可以沿x轴负方向滚动．
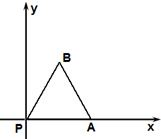精英家教网如图放置的边长为1的正三角形PAB沿x轴滚动，设顶点A（x，y）的纵坐标与横坐标的函数关系式是y=f（x），则f（x）在区间[-2，1]上的解析式是
 
；（说明：“正三角形PAB沿x轴滚动”包括沿x轴正方向和沿x轴负方向滚动．沿x轴正方向滚动指的是先以顶点A为中心顺时针旋转，当顶点B落在x轴上时，再以顶点B为中心顺时针旋转，如此继续；类似地，正三角形PAB也可以沿x轴负方向逆时针滚动）
如图放置的边长为1的正方形PABC沿x轴滚动．设顶点p（x，y）的轨迹方程是y=f（x），设f（x）的最小正周期为T，y=f（x）在其两个相邻零点间的图象与x轴所围区域的面积为S，则ST=
4（π+1）
4（π+1）
．（说明：“正方形PABC沿x轴滚动”包括沿x轴正方向和沿x轴负方向滚动．沿x轴正方向滚动指的是先以顶点A为中心顺时针旋转，当顶点B落在x轴上时，再以顶点B为中心顺时针旋转，如此继续．类似地，正方形PABC可以沿x轴负方向滚动．）
（2011•洛阳一模）如图放置的边长为1的正三角形ABC沿x轴的正方向滚动，设顶点A（x，y）的纵坐标与横坐标的函数关系是y=f（x）．则f（x）在两个相邻零点间的图象与x轴围成的面积是
2π
3
+
3
4
2π
3
+
3
4
．

如图所示，一个空间几何体的主视图和左视图都是边长为1的正方 形，俯视图是一个直径为1的圆，那么这个几何体的全面积为(  )

A．         B．            C．      D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网