题目内容
如图，在空间四边形ABCD中，E，F分别是AB，CD的中点．
（1）若AB=BC=CD=AD=AC=BD=2a，求EF的长；
（2）若AD=BC=2a，EF=
a，求异面直线AD与BC所成的角的余弦值．
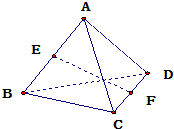
（1）若AB=BC=CD=AD=AC=BD=2a，求EF的长；
（2）若AD=BC=2a，EF=
| 3 |
（1）如图所示．
连接EC，ED．
∵AB=BC=AC=2a，
∴△ABC是等边三角形．
又AE=EB，∴CE⊥AB．
∴CE=
a．
同理DE=
a．
在△CED中，∵CE=ED=
a，CF=FD=a，
∴EF=
=
a；
（2）如图所示，取AC的中点M，连接EM，FM．
∵E，F分别是AB，CD的中点，
∴EM
BC，FM
AD．
∴∠EMF或其补角即为异面直线AD与BC所成的角，
又AD=BC=2a，
∴EM=FM=a．
在△EFM中，由余弦定理可得：cos∠EMF=
=
=-
．
∴异面直线AD与BC所成的角的余弦值为
．
连接EC，ED．
∵AB=BC=AC=2a，
∴△ABC是等边三角形．
又AE=EB，∴CE⊥AB．
∴CE=
| 3 |
同理DE=
| 3 |
在△CED中，∵CE=ED=
| 3 |
∴EF=
| CE2-CF2 |
| 2 |
（2）如图所示，取AC的中点M，连接EM，FM．
∵E，F分别是AB，CD的中点，
∴EM
| ∥ |
| . |
| 1 |
| 2 |
| ∥ |
| . |
| 1 |
| 2 |
∴∠EMF或其补角即为异面直线AD与BC所成的角，
又AD=BC=2a，
∴EM=FM=a．
在△EFM中，由余弦定理可得：cos∠EMF=
| EM2+FM2-EF2 |
| 2EM•FM |
a2×2-(
| ||
| 2×a2 |
| 1 |
| 2 |
∴异面直线AD与BC所成的角的余弦值为
| 1 |
| 2 |
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
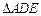沿DE折起，使二面角
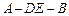的大小为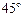
，此时点A在平面BCDE内的射影恰为点B，则M、N的连线与AE所成角的大小为 .
