Question

21.已知函数f(x)= x³－3ax²+2bx在点x =1处有极小值－1.试确定a、b的值.并求出f(x)的单调区间.

Answer 1

21.本小题考查函数和函数极值概念，考查运用导数研究函数性质的方法，以及分析和解决数学问题的能力.

解：由已知，可得

f(1) = 1－3a+2b = －1，          ①

又f′(1) = 3x²－6ax+2b，

∴f′(1) = 3－6a+2b = 0.             ②                        

由①②，可解得

                                              

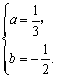
故函数的解析式为f(x) = x³―x²―x.

由此得        f′(x) =3x²―2x―1.                                

根据二次函数的性质，当时，f′(x)>0；

当时，f′(x)＜0.                                 

因此，在区间(－∞，)和(1，+∞)上，函数f(x)为增函数；在区间(，1)内，函数f(x)为减函数.