Question

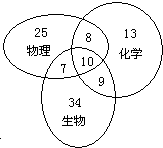
某校理科综合组成立物理，化学，生物兴趣小组，三个小组分别有50，40，60个成员，这些成员可以参加多少个兴趣小组，具体情况如图所示，随机选取一个成员．
（1）他属于至少2个小组的概率是多少？
（2）他属于不超过2个小组的概率是多少？

Answer 1

（1）由题意知本题是一个等可能事件的概率，
由图可知，三个兴趣小组总人数为106，用A表示事件：
选取的成员只属于一个小组，则：

.

A

表示：选取的成员属于至少两个小组
于是P(

.

A

)=1-P(A)=1-

25+13+34

106

=1-

72

106

=

17

53

…（4分）
因此，随机选取一个成员属于至少两个小组的概率是

17

53

…（6分）
（2）用B表示事件：选取的成员属于三个小组，则

.

B

表示：选取的成员不超过两个小组，
于是P(

.

B

)=1-P(B)=1-

10

106

=

48

53

…（10分）
所以随机选取一个成员属于不超过2个小组的概率是

48

53

…（12分）