题目内容
 如图,ABCD是边长为l的正方形,O为AD的中点,抛物线的顶点为O,且通过点C,则阴影部分的面积为( )
如图,ABCD是边长为l的正方形,O为AD的中点,抛物线的顶点为O,且通过点C,则阴影部分的面积为( )分析:以抛物线的顶点为原点,以平行于AB的直线为x轴建立平面直角坐标系,求出抛物线的方程,则阴影部分的面积等于正方形面积的一半减去抛物线与x=0,x=1,及x轴所围成的曲边梯形的面积.
解答:解:建立如图所示的坐标系,

因为正方形ABCD的边长为1,所以C(1,
),
设抛物线方程为y=ax2(a>0),则a=
,
所以,抛物线方程为y=
x2,
图中阴影部分的面积为:S=1×
x2dx=
-
=
-
=
.
故选D.

因为正方形ABCD的边长为1,所以C(1,
| 1 |
| 2 |
设抛物线方程为y=ax2(a>0),则a=
| 1 |
| 2 |
所以,抛物线方程为y=
| 1 |
| 2 |
图中阴影部分的面积为:S=1×
| 1 |
| 2 |
| -∫ | 1 0 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
| x3| | 1 0 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
故选D.
点评:本题考差了定积分,考查了定积分的简单应用,解答此题的关键是,正确建立平面直角坐标系,求出抛物线的方程,找出被积函数的原函数,从而运用微积分基本定理求解,此题是中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
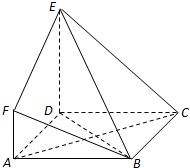 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°. 如图,ABCD是边长为a的菱形,且∠BAD=60°,△PAD为正三角形,且面PAD⊥面ABCD.
如图,ABCD是边长为a的菱形,且∠BAD=60°,△PAD为正三角形,且面PAD⊥面ABCD. 如图,ABCD是边长为2的正方形,面EAD⊥面ABCD,且EA=ED,EF∥AB,且EF=1,O是线段AD的中点,三棱锥F-OBC的体积为
如图,ABCD是边长为2的正方形,面EAD⊥面ABCD,且EA=ED,EF∥AB,且EF=1,O是线段AD的中点,三棱锥F-OBC的体积为 (2012•宁城县模拟)如图,ABCD是边长为1的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF.
(2012•宁城县模拟)如图,ABCD是边长为1的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF. 如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B';折痕与AB交于点E,以EB和EB’为邻边作平行四边形EB’MB.若以B为原点,BC所在直线为x轴建立直角坐标系(如下图):
如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B';折痕与AB交于点E,以EB和EB’为邻边作平行四边形EB’MB.若以B为原点,BC所在直线为x轴建立直角坐标系(如下图):