题目内容

已知在二阶矩阵M对应变换的作用下，四边形ABCD变成四边形A′B′C′D′，其中A（1，1），B（-1，1），C（-1，-1），A′（3，-3），B′（1，1），D′（-1，-1）．
（1）求出矩阵M；
（2）确定点D及点C′的坐标．
分析：（1）先设出矩阵M，利用待定系数法建立四个等式关系，解四元一次方程组即可；
（2）利用矩阵变换的定义建立等量关系即可求出C′，利用矩阵M的逆矩阵求出D点坐标即可．
解答：解：（1）设M=
ab
cd
，则有
ab
cd
1
1
=
3
-3
，
ab
cd
-1
1
=
1
1
，
故
a+6=3
c+d=-3
-a+b=1
-c+d=1
解得a=1，b=2，c=-2，d=-1，∴M=
12
-2-1
．（5分）
（2）由
12
-2-1
-1
-1
=
-3
3
知，C′（-3，3），
由
-
1
3
-
2
3
2
3
1
3
-1
-1
=
1
-1
知，D（1，-1）．（10分）
点评：本题主要考查了二阶矩阵的对应变换，属于基础题．
练习册系列答案
相关题目
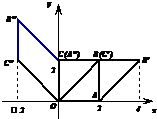精英家教网（Ⅰ）如图，正方形OABC在二阶矩阵M对应的切变变换作用下变为平行四边形OA′B′C′，平行四边形OA'B'C'在二阶矩阵N对应的旋转变换作用下变为平行四边形OA''B''C''，求将正方形OABC变为平行四边形OA''B''C''的变换对应的矩阵．
（Ⅱ）在直角坐标系xOy中，圆O的参数方程为
x=-
2
2
+rcosθ
y=-
2
2
+rsinθ
（θ为参数，r＞0）．以O为极点，x轴正半轴为极轴，并取相同的单位长度建立极坐标系，直线l的极坐标方程为ρsin(θ+
π
4
)=
2
2
．写出圆心的极标，并求当r为何值时，圆O上的点到直线l的最大距离为3．
（Ⅲ）已知a2+2b2+3c2=6，若存在实数a，b，c，使得不等式a+2b+3c＞|x+1|成立，求实数x的取值范围．
已知在二阶矩阵M对应变换的作用下，四边形ABCD变成四边形A′B′C′D′，其中A（1，1），B（-1，1），C（-1，-1），A′（3，-3），B′（1，1），D′（-1，-1）．
（1）求出矩阵M；
（2）确定点D及点C′的坐标．
已知在二阶矩阵M对应变换的作用下，四边形ABCD变成四边形A′B′C′D′，其中A（1，1），B（-1，1），C（-1，-1），A′（3，-3），B′（1，1），D′（-1，-1）．
（1）求出矩阵M；
（2）确定点D及点C′的坐标．
已知在二阶矩阵M对应变换的作用下，四边形ABCD变成四边形A′B′C′D′，其中A（1，1），B（-1，1），C（-1，-1），A′（3，-3），B′（1，1），D′（-1，-1）．
（1）求出矩阵M；
（2）确定点D及点C′的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网