题目内容
设函数f(x)=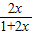 -
- ,[x]表示不超过x的最大整数,则y=[f(x)]的值域是( )
,[x]表示不超过x的最大整数,则y=[f(x)]的值域是( )A.{0,1}
B.{0,-1}
C.{-1,1}
D.{1,1}
【答案】分析:对f(x)进行化简,可得f(x)=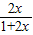 -
- =
= -
-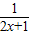 ,讨论其单调性,再分类讨论求出其值域,再根据定义,[x]表示不超过x的最大整数,进行求解;
,讨论其单调性,再分类讨论求出其值域,再根据定义,[x]表示不超过x的最大整数,进行求解;
解答:解:函数f(x)=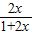 -
- ,[x]表示不超过x的最大整数,
,[x]表示不超过x的最大整数,
∴f(x)= -
-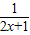 ,
,
若x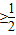 可得f(x)为增函数,当x→+∞时,f(x)=
可得f(x)为增函数,当x→+∞时,f(x)= ,
,
∴0≤f(x)< ;
;
若0≤x≤ ,f(x)为增函数,-
,f(x)为增函数,- ≤f(x)≤0
≤f(x)≤0
若- <x<0时,可得-
<x<0时,可得- <f(x)
<f(x)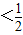 ,
,
若x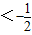 时,
时, <f(x)
<f(x)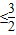 ,
,
综上- ≤f(x)≤
≤f(x)≤ ,
,
∵[x]表示不超过x的最大整数,
∴[f(x)]={0,1},
故选A;
点评:本题考查函数的值域,函数的单调性及其特点,考查学生分类讨论的思想,是中档题.
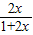 -
- =
= -
-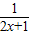 ,讨论其单调性,再分类讨论求出其值域,再根据定义,[x]表示不超过x的最大整数,进行求解;
,讨论其单调性,再分类讨论求出其值域,再根据定义,[x]表示不超过x的最大整数,进行求解;解答:解:函数f(x)=
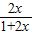 -
- ,[x]表示不超过x的最大整数,
,[x]表示不超过x的最大整数,∴f(x)=
 -
-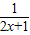 ,
,若x
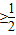 可得f(x)为增函数,当x→+∞时,f(x)=
可得f(x)为增函数,当x→+∞时,f(x)= ,
,∴0≤f(x)<
 ;
;若0≤x≤
 ,f(x)为增函数,-
,f(x)为增函数,- ≤f(x)≤0
≤f(x)≤0若-
 <x<0时,可得-
<x<0时,可得- <f(x)
<f(x)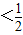 ,
,若x
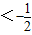 时,
时, <f(x)
<f(x)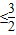 ,
,综上-
 ≤f(x)≤
≤f(x)≤ ,
,∵[x]表示不超过x的最大整数,
∴[f(x)]={0,1},
故选A;
点评:本题考查函数的值域,函数的单调性及其特点,考查学生分类讨论的思想,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012•重庆)设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
(2012•重庆)设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )