题目内容
AB、BC,CD是不在同一平面内的三条线段,经过它们中点的平面和AC的位置关系是
平行
平行
,和BD的位置关系是平行
平行
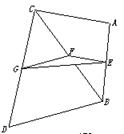
.分析:如图所示,利用三角形的中位线定理和线面平行的判定定理即可得出.
解答:解:如图所示.
设点E,F,G,H分别为棱AB、BC、CD、DA的中点.
则EF∥AC∥GH,而AC?平面EFGH,∴AC∥平面EFGH.
同理BD∥平面EFGH.
故答案分别为平行,平行.

设点E,F,G,H分别为棱AB、BC、CD、DA的中点.
则EF∥AC∥GH,而AC?平面EFGH,∴AC∥平面EFGH.
同理BD∥平面EFGH.
故答案分别为平行,平行.
点评:熟练掌握三角形的中位线定理和线面平行的判定定理是解题的关键.

练习册系列答案
相关题目
设
AB、BC、CD是不在同一平面内的三条线段,则经过它们中点的平面和直线AC的位置关系是[
]|
A .平行 |
B .相交 |
|
C .平行或相交 |
D .AC在此平面内 |