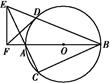
题目内容
如图, 是圆
是圆 的直径,
的直径, 是
是 延长线上的一点,
延长线上的一点, 是圆
是圆 的割线,过点
的割线,过点 作
作 的垂线,交直线
的垂线,交直线 于点
于点 ,交直线
,交直线  于点
于点 ,过点
,过点 作圆
作圆 的切线,切点为
的切线,切点为 .
.
(1)求证: 四点共圆;(2)若
四点共圆;(2)若 ,求
,求 的长.
的长.
(1)详见解析;(2)12
解析试题分析:(1)根据四边形的外角等于内角的对角时四点共圆,证
 问题即可得证。(2)由(1)可知
问题即可得证。(2)由(1)可知 四点共圆,则可根据切割弦定理求边长。
四点共圆,则可根据切割弦定理求边长。
试题解析:(1)
证明:连结 ,∵
,∵ 是圆
是圆 的直径,
的直径,
∴
在 和
和 中,
中,
又∵ ∴
∴

∴ 四点共圆. 5分
四点共圆. 5分
(2)∵ 四点共圆,∴
四点共圆,∴
∵ 是圆
是圆 的切线,∴
的切线,∴ ∴
∴
又因为 ∴
∴
∴ . 10分
. 10分
考点:1四点共圆;2切割弦定理。

练习册系列答案
相关题目




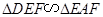 ;(2)EF//CB.
;(2)EF//CB.