题目内容
已知a∈R,函数f(x)=x2|x﹣a|.
(1)当a=2时,求使f(x)=x成立的x的集合;
(2)求函数y=f(x)在区间[1,2]上的最小值.
(1)当a=2时,求使f(x)=x成立的x的集合;
(2)求函数y=f(x)在区间[1,2]上的最小值.
解:(Ⅰ)由题意,f(x)=x2|x﹣2|
当x<2时,由f(x)=x2(2﹣x)=x,解得x=0或x=1;
当x≥2时,由f(x)=x2(x﹣2)=x,解得x=1+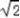 .
.
综上,所求解集为{0,1,1+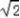 }
}
(Ⅱ)设此最小值为m.
①当a≤1时,在区间[1,2]上,f(x)=x3﹣ax2,
∵f′(x)=3x2﹣2ax=3x(x﹣ a)>0,x∈(1,2),
a)>0,x∈(1,2),
则f(x)是区间[1,2]上的增函数,
∴m=f(1)=1﹣a.
②当1<a≤2时,在区间[1,2]上,f(x)=x2|x﹣a|≥0,由f(a)=0知m=f(a)=0.
③当a>2时,在区间[1,2]上,f(x)=ax2﹣x3f′(x)=2ax﹣3x2=3x( a﹣x).
a﹣x).
若a≥3,在区间(1,2)上,f'(x)>0,则f(x)是区间[1,2]上的增函数,
∴m=f(1)=a﹣1.
若2<a<3,则1< a<2.
a<2.
当1<x< a时,f'(x)>0,则f(x)是区间[1,
a时,f'(x)>0,则f(x)是区间[1, a]上的增函数,
a]上的增函数,
当 a<x<2时,f'(x)<0,则f(x)是区间[
a<x<2时,f'(x)<0,则f(x)是区间[  a,2]上的减函数,
a,2]上的减函数,
因此当2<a<3时,故m=f(1)=a﹣1或m=f(2)=4(a﹣2).
当2<a≤ 时,4(a﹣2)≤a﹣1,故m=f(2)=4(a﹣2),
时,4(a﹣2)≤a﹣1,故m=f(2)=4(a﹣2),
当 <a<3时,4(a﹣2)<a﹣1,故m=f(1)=a﹣1.
<a<3时,4(a﹣2)<a﹣1,故m=f(1)=a﹣1.
总上所述,所求函数的最小值m=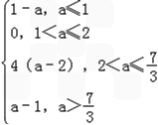 .
.
当x<2时,由f(x)=x2(2﹣x)=x,解得x=0或x=1;
当x≥2时,由f(x)=x2(x﹣2)=x,解得x=1+
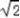 .
.综上,所求解集为{0,1,1+
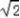 }
} (Ⅱ)设此最小值为m.
①当a≤1时,在区间[1,2]上,f(x)=x3﹣ax2,
∵f′(x)=3x2﹣2ax=3x(x﹣
 a)>0,x∈(1,2),
a)>0,x∈(1,2),则f(x)是区间[1,2]上的增函数,
∴m=f(1)=1﹣a.
②当1<a≤2时,在区间[1,2]上,f(x)=x2|x﹣a|≥0,由f(a)=0知m=f(a)=0.
③当a>2时,在区间[1,2]上,f(x)=ax2﹣x3f′(x)=2ax﹣3x2=3x(
 a﹣x).
a﹣x).若a≥3,在区间(1,2)上,f'(x)>0,则f(x)是区间[1,2]上的增函数,
∴m=f(1)=a﹣1.
若2<a<3,则1<
 a<2.
a<2.当1<x<
 a时,f'(x)>0,则f(x)是区间[1,
a时,f'(x)>0,则f(x)是区间[1, a]上的增函数,
a]上的增函数,当
 a<x<2时,f'(x)<0,则f(x)是区间[
a<x<2时,f'(x)<0,则f(x)是区间[  a,2]上的减函数,
a,2]上的减函数,因此当2<a<3时,故m=f(1)=a﹣1或m=f(2)=4(a﹣2).
当2<a≤
 时,4(a﹣2)≤a﹣1,故m=f(2)=4(a﹣2),
时,4(a﹣2)≤a﹣1,故m=f(2)=4(a﹣2),当
 <a<3时,4(a﹣2)<a﹣1,故m=f(1)=a﹣1.
<a<3时,4(a﹣2)<a﹣1,故m=f(1)=a﹣1.总上所述,所求函数的最小值m=
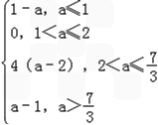 .
. 
练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目