题目内容
已知平面向量![]() 满足
满足![]() ,且
,且![]() 与
与![]() 的夹角为135°,
的夹角为135°,![]() 与
与![]() 的夹角为120°,
的夹角为120°,![]() ,则
,则![]() = .
= .
考点:
平面向量数量积坐标表示的应用;向量在几何中的应用.
分析:
由已知![]() ,可知三个向量首尾相接后,构成一个三角形,且
,可知三个向量首尾相接后,构成一个三角形,且![]() 与
与![]() 的夹角为135°,
的夹角为135°,![]() 与
与![]() 的夹角为120°,
的夹角为120°,![]() ,可以得到三角形的两个内角和一边的长,利用正弦定理,可求出向量
,可以得到三角形的两个内角和一边的长,利用正弦定理,可求出向量![]() 对应边的长度.
对应边的长度.
解答:
解:∵![]()
∴三个向量首尾相接后,构成一个三角形
且![]() 与
与![]() 的夹角为135°,
的夹角为135°,![]() 与
与![]() 的夹角为120°,
的夹角为120°,![]() ,
,
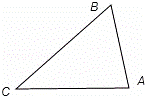
故所得三角形如下图示:
其中∠C=45°,∠A=60°,AB=2
∴![]() =
=![]() =
=![]()
故答案为:![]()
点评:
求向量的模有如下方法:若已知向量的坐标,或向量起点和终点的坐标,则![]() 或
或![]() ;若未知向量的坐标,只是已知条件中有向量的模及夹角,则求向量的模时,主要是根据向量数量的数量积计算公式,求出向量模的平方,即向量的平方,再开方求解.将表示向量的有向线段纳入三角形,解三角形求出对应边长,从而得到向量的模.
;若未知向量的坐标,只是已知条件中有向量的模及夹角,则求向量的模时,主要是根据向量数量的数量积计算公式,求出向量模的平方,即向量的平方,再开方求解.将表示向量的有向线段纳入三角形,解三角形求出对应边长,从而得到向量的模.

练习册系列答案
相关题目
 满足
满足 ,且
,且 与
与 的夹角为120°,
的夹角为120°, ,则
,则 的取值范围是
.
的取值范围是
. 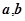 满足
满足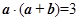 ,且
,且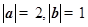 ,则向量
,则向量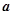 与
与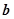 的夹角为
的夹角为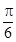 B.
B.
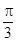 C.
C. 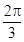 D.
D. 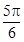
 满足
满足 ,且
,且 与
与 的夹角为120°,
的夹角为120°, ,则
,则 的取值范围是 ▲ .
的取值范围是 ▲ .