题目内容
如下图所示,已知正三棱锥S—ABC的高SO=h,斜高SM=l,求经过SO的中点平行于底面的截面△A′B′C′的面积.
思路解析：平行于棱锥底面的截面和底面多边形相似,面积之比等于对应高的平方比.
解：连结OA、OM,
在Rt△SOM中,OM=
.
因为棱锥S—ABC是正棱锥,所以点O是正△ABC的中心,AB=2AM=2OMtan60°=2
.
所以S△ABC=
AB2=
·4·3(l2-h2)=3
(l2-h2).
根据一般三棱锥的截面性质,有
,
所以S△A′B′C′=
(l2-h2)(cm2).
练习册系列答案
天天向上口算本系列答案
相关题目
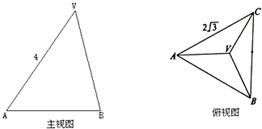（2010•汕头模拟）已知正三棱锥V-ABC的主视图、俯视图如下图所示，其中
的主视图、俯视图如下图所示，其中VA=4，AC=
,则该三棱锥的左视图的面积； 
D．
，则该三棱锥的左视图的面积为（
）
D. 