题目内容

数列{a_n}、{b_n}满足a_nb_n=1，a_n=n²+3n+2，则{b_n}的前n项和为________．

$\text{[math]}$
分析：先根据a_nb_n=1，a_n=n²+3n+2求出数列{b_n}的通项公式，得到b_n= $\text{[math]}$ ，再利用裂项相消法求数列的前n项和即可．
解答：∵a_nb_n=1，a_n=n²+3n+2，
∴b_n= $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$
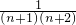∴{b_n}的前n项和S_n=（ $\text{[math]}$ ）+（ $\text{[math]}$ ）+（ $\text{[math]}$ ）+…+（ $\text{[math]}$ ）
= $\text{[math]}$ + $\text{[math]}$ + $\text{[math]}$ +…+ $\text{[math]}$
= $\text{[math]}$
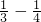故答案为 $\text{[math]}$
点评：本题主要考查了裂项相消法求数列的前n项和，考查了学生的观察能力以及转换能力，属于数列的常规题．

练习册系列答案

中考高手系列答案

新支点中考经典系列答案

中考零距离突破系列答案

中考信息猜想卷系列答案

中考专辑精通中考系列答案

中考锦囊系列答案

中考状元系列答案

中考总复习系列答案

掌控中考系列答案

68所名校图书毕业升学全真模拟试卷系列答案

相关题目

已知数列{a_n}中，其前n项和为S_n，满足S_n=2a_n-1，n∈N*，数列{b_n}满足bn=1-log

an，n∈N*
（1）求数列{a_n}、{b_n}的通项公式；
（2）设数列{a_nb_n}的n项和为T_n，求T_n．

设集合W由满足下列两个条件的数列{a_n}构成：①

＜an+1；②存在实数M，使a_n≤M．（n为正整数）
（Ⅰ）在只有5项的有限数列{a_n}、{b_n}中，其中a₁=1，a₂=2，a₃=3，a₄=4，a₅=5；b₁=1，b₂=4，b₃=5，b₄=4，b₅=1；试判断数列{a_n}、{b_n}是否为集合W中的元素；
（Ⅱ）设{c_n}是各项为正数的等比数列，S_n是其前n项和，c3=

，试证明{S_n}∈W，并写出M的取值范围；
（Ⅲ）设数列{d_n}∈W，对于满足条件的M的最小值M₀，都有d_n≠M₀（n∈N^*）．求证：数列{d_n}单调递增．

数列{a_n}、{b_n}满足a_nb_n=1，an=n2+n，则数列{b_n}的前10项和为

在数列{a_n}，{b_n}中，对任何正整数n都有：a1b1+a2b2+a3b3+…+an-1bn-1+anbn=(n-1)•2n+1
（1）若数列{b_n}是首项为1和公比为2的等比数列，求数列{a_n}，{b_n}的通项公式；
（2）若数列{a_n}是首项为a₁，公差为d等差数列（a₁•d≠0），求数列{b_n}的通项公式；
（3）在（2）的条件下，判断数列{b_n}是否为等比数列？并说明理由．

（2010•肇庆二模）已知等差数列{a_n}的各项均为正数，a₁=3，前n项和为S_n，{b_n}是等比数列，b₁=1，且b₂S₂=64，b₃S₃=960．
（1）求数列{a_n}与{b_n}的通项公式；
（2）求证：

对一切n∈N*都成立．