题目内容
已知函数f(x)= ax3-
ax3- x2+cx+d(a、c、d∈R)满足f(0)=0,f′(1)=0且f′(x)≥0在R上恒成立.
x2+cx+d(a、c、d∈R)满足f(0)=0,f′(1)=0且f′(x)≥0在R上恒成立.(1)求a、c、d的值;
(2)若h(x)=
 x2-bx+
x2-bx+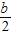 -
- ,解不等式f′(x)+h(x)<0.
,解不等式f′(x)+h(x)<0.
【答案】分析:(1)先利用f(0)=0,f′(1)=0得到d的值和a,c的关系式,然后利用一元二次不等式大于等于0恒成立时a>0,△≤0,求出a的值,从而问题得解;
(2)结合(1)和已知,先将不等式化简,即x2-(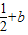 )x+
)x+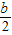 <0,然后根据解一元二次不等式的步骤,先令x2-(
<0,然后根据解一元二次不等式的步骤,先令x2-(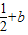 )x+
)x+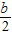 =0,解得x=b或x=
=0,解得x=b或x= ,然后根据b与
,然后根据b与 的大小关系分类讨论,进行解答.
的大小关系分类讨论,进行解答.
解答:解:(1)∵f(x)= ax3-
ax3- x2+cx+d,
x2+cx+d,
∴f′(x)=ax2- x+c,
x+c,
∵f(0)=0,f′(1)=0,
∴d=0,a- +c=0,
+c=0,
即d=0,c=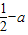 ,
,
从而f′(x)=ax2- x+
x+ -a.
-a.
∵f′(x)≥0在R上恒成立,
∴a>0,△=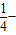 4a(
4a( -a)≤0,
-a)≤0,
即a>0,(a- )2≤0,
)2≤0,
解得a= ,c=
,c= ,d=0,
,d=0,
(2)由(1)知,f′(x)= x2-
x2- x+
x+ ,
,
∵h(x)= x2-bx+
x2-bx+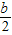 -
- ,
,
∴不等式f′(x)+h(x)<0化为 x2-
x2- x+
x+ +
+ x2-bx+
x2-bx+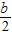 -
- <0,
<0,
即x2-(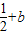 )x+
)x+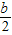 <0,
<0,
∴(x- )(x-b)<0,
)(x-b)<0,
①若b> ,则所求不等式的解为
,则所求不等式的解为 <x<b;
<x<b;
②若b= ,则所求不等式的解为空集;
,则所求不等式的解为空集;
③若b< ,则所求不等式的解为b<x<
,则所求不等式的解为b<x< .
.
综上所述,当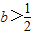 时,所求不等式的解为
时,所求不等式的解为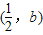 ;当
;当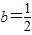 时,所求不等式的解为∅;当
时,所求不等式的解为∅;当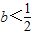 时,所求不等式的解为
时,所求不等式的解为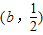 .
.
点评:此题是导数与不等式的综合问题,同时考查了一元二次不等式大于等于0恒成立的条件和分类讨论的数学思想.
(2)结合(1)和已知,先将不等式化简,即x2-(
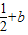 )x+
)x+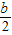 <0,然后根据解一元二次不等式的步骤,先令x2-(
<0,然后根据解一元二次不等式的步骤,先令x2-(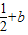 )x+
)x+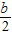 =0,解得x=b或x=
=0,解得x=b或x= ,然后根据b与
,然后根据b与 的大小关系分类讨论,进行解答.
的大小关系分类讨论,进行解答.解答:解:(1)∵f(x)=
 ax3-
ax3- x2+cx+d,
x2+cx+d,∴f′(x)=ax2-
 x+c,
x+c,∵f(0)=0,f′(1)=0,
∴d=0,a-
 +c=0,
+c=0,即d=0,c=
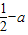 ,
,从而f′(x)=ax2-
 x+
x+ -a.
-a.∵f′(x)≥0在R上恒成立,
∴a>0,△=
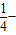 4a(
4a( -a)≤0,
-a)≤0,即a>0,(a-
 )2≤0,
)2≤0,解得a=
 ,c=
,c= ,d=0,
,d=0,(2)由(1)知,f′(x)=
 x2-
x2- x+
x+ ,
,∵h(x)=
 x2-bx+
x2-bx+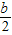 -
- ,
,∴不等式f′(x)+h(x)<0化为
 x2-
x2- x+
x+ +
+ x2-bx+
x2-bx+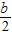 -
- <0,
<0,即x2-(
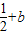 )x+
)x+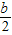 <0,
<0,∴(x-
 )(x-b)<0,
)(x-b)<0,①若b>
 ,则所求不等式的解为
,则所求不等式的解为 <x<b;
<x<b;②若b=
 ,则所求不等式的解为空集;
,则所求不等式的解为空集;③若b<
 ,则所求不等式的解为b<x<
,则所求不等式的解为b<x< .
.综上所述,当
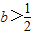 时,所求不等式的解为
时,所求不等式的解为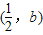 ;当
;当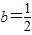 时,所求不等式的解为∅;当
时,所求不等式的解为∅;当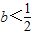 时,所求不等式的解为
时,所求不等式的解为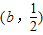 .
.点评:此题是导数与不等式的综合问题,同时考查了一元二次不等式大于等于0恒成立的条件和分类讨论的数学思想.

练习册系列答案
相关题目