题目内容
下列函数中,满足“对任意x1,x2∈(0,+∞),都有
>0成立”的是( )
| f(x1)-f(x2) |
| x1-x2 |
A.f(x)=
| B.f(x)=ln(x+1) | C.f(x)=(
| D.f(x)=|x-1| |
由题意:对任意x1,x2∈(0,+∞),都有
>0成立,知f(x)在(0,+∞)上单调递增,
f(x)=
在(0,+∞)上递减,故排除A;
f(x)=(
)x在(0,+∞)上递减,故排除C;
f(x)=|x-1|在(-∞,1]上递减,在[1,+∞)上递增,所以f(x)在(0,+∞)上不单调,故排除D;
而f(x)=ln(1+x)在(0,+∞)上递增,
故选B.
| f(x1)-f(x2) |
| x1-x2 |
f(x)=
| 1 |
| x |
f(x)=(
| 1 |
| 2 |
f(x)=|x-1|在(-∞,1]上递减,在[1,+∞)上递增,所以f(x)在(0,+∞)上不单调,故排除D;
而f(x)=ln(1+x)在(0,+∞)上递增,
故选B.

练习册系列答案
相关题目
 中,满足“对任意
中,满足“对任意 ,
,
 (0,
(0, ),当
),当 >
> 的是(
)
的是(
)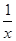 B.
B.
 C .
C . D.
D.