Question

已知二次函数f(x)=ax²+bx+c和一次函数g(x)=-bx,其中a,b,c是实数,且满足a＞b＞c,a+b+c=0.

(1)求证:y=f(x)与y=g(x)的图象交于不同的两点A,B;

(2)求证:方程f(x)-g(x)=0的两根都小于2;

(3)求有向线段AB在x轴上的射影A₁B₁的长度的变化范围.

Answer 1

解析:∵a＞b＞c,a+b+c=0,

∴a＞0,c＜0.

(1)证明:由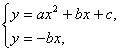消去y,得

ax²+2bx+c=0.①

∴两图象交于不同的两点A,B?方程①有两个不同实数解.

∵a＞0,c＜0,

∴Δ＞0,∴方程①有两个不同的实根.

(2)证明:令F(x)=ax²+2bx+c.

∴方程f(x)-g(x)=0的两根都小于2?y=F(x)的图象与x轴的交点在点(2,0)的左侧.

∵a＞0,

∴只需证对称轴x=-＜2,且F(2)＞0.

而a＞b＞c,a+b+c=0,

∴a+2b＞0,∴-＜＜2.

又F(2)=4a+4b+c=3(a+b)=3(-c)＞0,

故命题(2)得证.

(3)设A(x₁,y₁),B(x₂,y₂),

则A₁(x₁,0),B₁(x₂,0).

∴|A₁B₁|=|x₁-x₂|

=.

∵a＞b＞c,a+b+c=0,

∴2a+c＞0,且a+2c＜0.

∴-2＜＜-,

∴|A₁B₁|∈().