题目内容
已知f(x)是定义在R上的不恒为零的函数,且对于任意的a、b∈R都满足f(ab)=af(b)+bf(a).
(1)求f(0)、f(1)的值;
(2)判断f(x)的奇偶性.
答案:
解析:
提示:
解析:
|
解:(1)令a=b=0,得f(0)=0;令a=b=1,得f(1)=0. (2)f(x)为奇函数.因为f(-x)=f(-1·x)=-f(x)+xf(-1),而0=f(1)=f[(-1)×(-1)]=-f(-1)-f(-1),因此f(-1)=0,所以f(-x)=-f(x),即f(x)为奇函数. 点评:抽象函数的表现形式比较抽象,直接求解思路难寻,因此我们在解决此类问题时可以采用赋值法,即通过化抽象为具体的方法,经过运算与推理,最后得出结论. |
提示:
|
本题中的函数是没有给出函数解析式的抽象函数,由于这种表现形式比较抽象,使得直接求解思路难寻,因此我们可以采用赋值法. |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ) =
f(x)-f(y)
) =
f(x)-f(y) 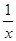 ) <2
) <2  ∪
∪ 上的奇函数,当
上的奇函数,当 时,f (x)的图象如图所示,那么f (x)的值域是
时,f (x)的图象如图所示,那么f (x)的值域是
