题目内容
若函数f(x)=ex+ln x,g(x)=e-x+ln x,h(x)=e-x-ln x的零点依次为a,b,c,则a,b,c的大小依次为( )
| A、a>b>c | B、a>c>b | C、c>a>b | D、c>b>a |
分析:分别由f(x)=0,g(x)=0,h(x)=0,得到两个函数关系,利用数形结合即可得到函数零点a,b,c的大小关系.
解答:解:∵f(x)=ex+ln x,g(x)=e-x+ln x,h(x)=e-x-ln x,
∴由f(x)=0,g(x)=0,h(x)=0,
得ex+ln x=0,g(x)=e-x+ln x=0,h(x)=e-x-ln x=0,
即-ex=ln x,-e-x=ln x,e-x=ln x,
分别作出函数y=-ex,y=-e-x,y=-e-x,y=ln x的图象如图:
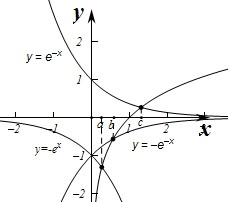 则由图象可知0<a<b<1<c,
则由图象可知0<a<b<1<c,
即c>b>a,
故选:D.
∴由f(x)=0,g(x)=0,h(x)=0,
得ex+ln x=0,g(x)=e-x+ln x=0,h(x)=e-x-ln x=0,
即-ex=ln x,-e-x=ln x,e-x=ln x,
分别作出函数y=-ex,y=-e-x,y=-e-x,y=ln x的图象如图:
 则由图象可知0<a<b<1<c,
则由图象可知0<a<b<1<c,即c>b>a,
故选:D.
点评:本题主要考查函数零点的大小判断,根据方程和函数之间的关系,将方程转化为两个函数的交点问题是解决本题的关键,注意利用数形结合的数学思想.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
若函数f(x)=ex+ae-x,其导函数是奇函数,并且曲线y=f(x)的一条切线的斜率是
,则切点的横坐标是( )
| 3 |
| 2 |
A、-
| ||
| B、-ln2 | ||
C、
| ||
| D、ln2 |