题目内容
在△ABC中,sin(C-A)=1,sinB= .
.(I)求sinA的值;
(II)设AC=
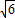 ,求△ABC的面积.
,求△ABC的面积.
【答案】分析:(I)利用sin(C-A)=1,求出A,C关系,通过三角形内角和结合sinB= ,求出sinA的值;
,求出sinA的值;
(II)通过正弦定理,利用(I)及AC=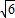 ,求出BC,求出sinC,然后求△ABC的面积.
,求出BC,求出sinC,然后求△ABC的面积.
解答: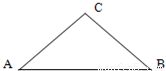 解:(Ⅰ)因为sin(C-A)=1,所以
解:(Ⅰ)因为sin(C-A)=1,所以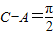 ,且C+A=π-B,
,且C+A=π-B,
∴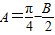 ,
,
∴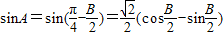 ,
,
∴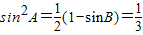 ,
,
又sinA>0,∴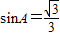
(Ⅱ)如图,由正弦定理得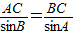
∴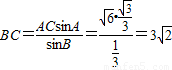 ,
,
又sinC=sin(A+B)=sinAcosB+cosAsinB=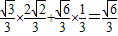
∴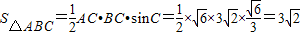
点评:本小题主要考查三角恒等变换、正弦定理、解三角形等有关知识,考查运算求解能力.
 ,求出sinA的值;
,求出sinA的值;(II)通过正弦定理,利用(I)及AC=
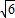 ,求出BC,求出sinC,然后求△ABC的面积.
,求出BC,求出sinC,然后求△ABC的面积.解答:
 解:(Ⅰ)因为sin(C-A)=1,所以
解:(Ⅰ)因为sin(C-A)=1,所以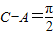 ,且C+A=π-B,
,且C+A=π-B,∴
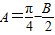 ,
,∴
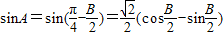 ,
,∴
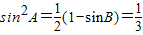 ,
,又sinA>0,∴
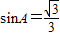
(Ⅱ)如图,由正弦定理得
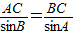
∴
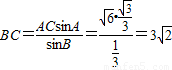 ,
,又sinC=sin(A+B)=sinAcosB+cosAsinB=
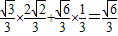
∴
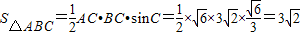
点评:本小题主要考查三角恒等变换、正弦定理、解三角形等有关知识,考查运算求解能力.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
在△ABC中,“sin(A-B)cosB+cos(A-B)sinB≥1”是“△ABC是直角三角形”的( )
| A、充分不必要条件 | B、必要不充分条件 | C、充分必要条件 | D、既不充分也不必要条件 |