题目内容
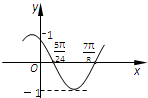已知函数f（x）=Asin（ωx+?）（其中A＞0，ω＞0，-π＜?≤π）的部分图象如图所示，与x轴的两个交点的横坐标分别为| 5π |
| 24 |
| 7π |
| 8 |
| 2π |
| 3 |
| 2π |
| 3 |
分析：根据已知条件，两个相邻的零点的差距为
-
=
，恰好是半个周期，得到函数的周期为
．再根据结论：函数
y=Asin（ωx+?）图象的两条相邻对称轴的距离等于半个周期，得到函数f（x）的图象的相邻两条对称轴之间的距离
．
| 7π |
| 8 |
| 5π |
| 24 |
| 2π |
| 3 |
| 4π |
| 3 |
y=Asin（ωx+?）图象的两条相邻对称轴的距离等于半个周期，得到函数f（x）的图象的相邻两条对称轴之间的距离
| 2π |
| 3 |
解答：解：∵函数图象与x轴的两个交点的横坐标分别为
、
，且它们是相邻的两个零点，
∴函数的周期为T=2（
-
）=
又∵函数y=Asin（ωx+?）图象的两条相邻对称轴的距离等于半个周期，
∴函数f（x）的图象的相邻两条对称轴之间的距离是
T=
．
故答案为：
| 5π |
| 24 |
| 7π |
| 8 |
∴函数的周期为T=2（
| 7π |
| 8 |
| 5π |
| 24 |
| 4π |
| 3 |
又∵函数y=Asin（ωx+?）图象的两条相邻对称轴的距离等于半个周期，
∴函数f（x）的图象的相邻两条对称轴之间的距离是
| 1 |
| 2 |
| 2π |
| 3 |
故答案为：
| 2π |
| 3 |
点评：本题给出函数f（x）=Asin（ωx+?）的部分图象，并且知道它与x轴的两个相邻交点的横坐标，求函数相邻对称轴的距离，着重考查了函数f（x）=Asin（ωx+?）的对称性与周期等知识点，属于基础题．
练习册系列答案
相关题目