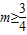题目内容
如果方程（x-1）（x2-2x+m）=0的三个根可以作为一个三角形的三条边长，那么实数m的取值范围是（ ）
| A．0≤m≤1 | B．
| C．
| D．m≥
|
∵方程（x-1）（x2-2x+m）=0的有三根，
∴x1=1，x2-2x+m=0有根，方程x2-2x+m=0的△=4-4m≥0，得m≤1．
又∵原方程有三根，且为三角形的三边长．
∴有x2+x3＞x1=1，|x2-x3|＜x1=1，由根系关系得x2x3=m，x2+x3=2＞1成立，；
当|x2-x3|＜1时，两边平方得：（x2+x3）2-4x2x3＜1．
代入相应数据得4-4m＜1．解得，m＞
．
∴
＜m≤1．
故选B．
∴x1=1，x2-2x+m=0有根，方程x2-2x+m=0的△=4-4m≥0，得m≤1．
又∵原方程有三根，且为三角形的三边长．
∴有x2+x3＞x1=1，|x2-x3|＜x1=1，由根系关系得x2x3=m，x2+x3=2＞1成立，；
当|x2-x3|＜1时，两边平方得：（x2+x3）2-4x2x3＜1．
代入相应数据得4-4m＜1．解得，m＞
| 3 |
| 4 |
∴
| 3 |
| 4 |
故选B．
练习册系列答案
快捷英语周周练系列答案
相关题目
＜m≤1 C.
≤m≤1 Dm≥
