题目内容
已知椭圆以坐标原点为中心,坐标轴为对称轴,且该椭圆以抛物线y2=16x的焦点P为其一个焦点,以双曲线 的焦点Q为顶点.
的焦点Q为顶点.(1)求椭圆的标准方程;
(2)已知点A(-1,0),B(1,0),且C、D分别为椭圆的上顶点和右顶点,点M是线段CD上的动点,求
 的取值范围.
的取值范围.
【答案】分析:(1)由题设条件知P(4,0),点Q(5,0),设椭圆的标准方程为 ,且a=5,c=4,由此能求出椭圆的标准方程.
,且a=5,c=4,由此能求出椭圆的标准方程.
(2)设M(x,y),线段CD方程为 ,即
,即 ,由点M是线段CD上,知
,由点M是线段CD上,知 ,由此能求出
,由此能求出 的取值范围.
的取值范围.
解答:解:(1)由已知得点P为(4,0),点Q为(5,0)…(2分)
∴可设椭圆的标准方程为 ,且a=5,c=4…(3分)
,且a=5,c=4…(3分)
∴b2=25-16=9,故椭圆的标准方程为 .…(5分)
.…(5分)
(2)设M(x,y),线段CD方程为 ,即
,即 …(7分)
…(7分)
∵点M是线段CD上,∴
又 ,
,
∴ ,…(10分)
,…(10分)
将 代入得:
代入得:
∴ …(12分)
…(12分)
∵0≤x≤5,
∴ 的最大值为24,
的最大值为24, 的最小值为
的最小值为 .
.
∴ 的取值范围是
的取值范围是 .…(14分)
.…(14分)
点评:本题考查椭圆的标准方程的求法和求 的取值范围.考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.
的取值范围.考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.
 ,且a=5,c=4,由此能求出椭圆的标准方程.
,且a=5,c=4,由此能求出椭圆的标准方程.(2)设M(x,y),线段CD方程为
 ,即
,即 ,由点M是线段CD上,知
,由点M是线段CD上,知 ,由此能求出
,由此能求出 的取值范围.
的取值范围.解答:解:(1)由已知得点P为(4,0),点Q为(5,0)…(2分)
∴可设椭圆的标准方程为
 ,且a=5,c=4…(3分)
,且a=5,c=4…(3分)∴b2=25-16=9,故椭圆的标准方程为
 .…(5分)
.…(5分)(2)设M(x,y),线段CD方程为
 ,即
,即 …(7分)
…(7分)∵点M是线段CD上,∴

又
 ,
,∴
 ,…(10分)
,…(10分)将
 代入得:
代入得:
∴
 …(12分)
…(12分)∵0≤x≤5,
∴
 的最大值为24,
的最大值为24, 的最小值为
的最小值为 .
.∴
 的取值范围是
的取值范围是 .…(14分)
.…(14分)点评:本题考查椭圆的标准方程的求法和求
 的取值范围.考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.
的取值范围.考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答. 
练习册系列答案
相关题目
 的焦点
的焦点 为其一个焦点,以双曲线
为其一个焦点,以双曲线 的焦点
的焦点 为顶点。
为顶点。 ,且C、D分别为椭圆的上顶点和右顶点,点M是线段CD上的动点,求
,且C、D分别为椭圆的上顶点和右顶点,点M是线段CD上的动点,求 的取值范围。
的取值范围。 的焦点
的焦点 为其一个焦点,以双曲线
为其一个焦点,以双曲线 的焦点
的焦点 为顶点。
为顶点。 ,且
,且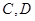 分别为椭圆的上顶点和右顶点,点
分别为椭圆的上顶点和右顶点,点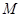 是线段
是线段 上的动点,求
上的动点,求 的取值范围。
的取值范围。